
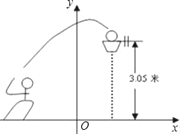
【题目】如图,一位篮球运动员跳起投篮,球沿抛物线y=﹣![]() x2+3.5运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
x2+3.5运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:①都是直角三角形;②都是锐角三角形;③都是钝角三角形.
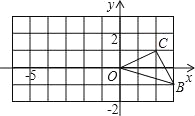
(2)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
①以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
②分别写出B、C两点的对应点B′、C′的坐标;
③如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
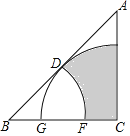
【题目】如图,已知等腰直角三角形ABC,∠ACB=90°,D是斜边AB的中点,且AC=BC=16分米,以点B为圆心,BD为半径画弧,交BC于点F,以点C为圆心,CD为半径画弧,分别交AB、BC于点E、G.求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:![]() =1.41,
=1.41,![]() =1.73).
=1.73).
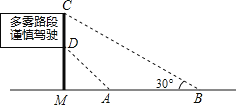
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA’B’C’的位置.若OB=![]() ,∠C=120°,则点B’的坐标为( )
,∠C=120°,则点B’的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
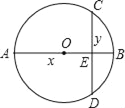
【题目】善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com