
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
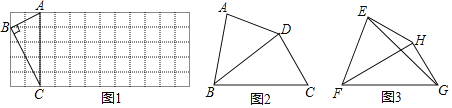
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
【答案】(1)见解析;(2)证明见解析;(3)FH=2![]() .
.
【解析】
(1)先求出AB,BC,AC,再分情况求出CD或AD,即可画出图形;
(2)先判断出∠A+∠ADB=140°=∠ADC,即可得出结论;
(3)先判断出△FEH∽△FHG,得出FH2=FEFG,再判断出EQ=![]() FE,继而求出FGFE=8,即可得出结论.
FE,继而求出FGFE=8,即可得出结论.
(1)由图1知,AB=![]() ,BC=2
,BC=2![]() ,∠ABC=90°,AC=5,
,∠ABC=90°,AC=5,
∵四边形ABCD是以AC为“相似对角线”的四边形,
当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,
∴![]() 或
或![]() ,
,
∴CD=10或CD=2.5
同理:当∠CAD=90°时,AD=2.5或AD=10,
(2)∵∠ABC=80°,BD平分∠ABC,
∴∠ABD=∠DBC=40°,
∴∠A+∠ADB=140°
∵∠ADC=140°,
∴∠BDC+∠ADB=140°,
∴∠A=∠BDC,
∴△ABD∽△BDC,
∴BD是四边形ABCD的“相似对角线”;

(3)如图3,
∵FH是四边形EFGH的“相似对角线”,
∴△EFH与△HFG相似,
∵∠EFH=∠HFG,
∴△FEH∽△FHG,
∴![]() ,
,
∴FH2=FEFG,
过点E作EQ⊥FG于Q,
∴EQ=FEsin60°=![]() FE,
FE,
∵![]() FG×EQ=2
FG×EQ=2![]() ,
,
∴![]() FG×
FG×![]() FE=2
FE=2![]() ,
,
∴FGFE=8,
∴FH2=FEFG=8,
∴FH=2![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
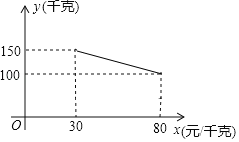
【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
(1)直接写出y与x之间的函数关系式;
(2)如果该超市销售这种商品每天获得3900元的利润,那么该商品的销售单价为多少元?
(3)设每天的总利润为w元,当销售单价定为多少元时,该超市每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
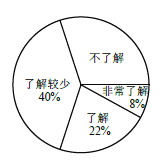

(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程m2x2+(2m﹣1)x+1=0有两个不相等的根a,b,
(1)求实数m的取值范围;
(2)是否存在实数m,使方程的两个实数根互为相反数?如果存在求出m的值,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
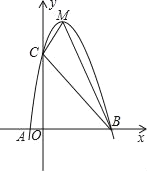
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在![]() 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则![]() = ,点E的坐标是 .
= ,点E的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
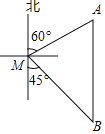
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com