
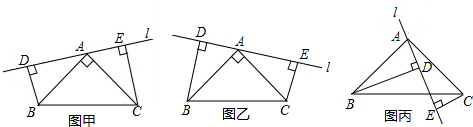
���� ��1�����������Եó���D=��E=90�㣬��4=��3���Ϳ���֤����ADB�ա�CEA�Ϳ��Եó�BD=AE��AD=CE����DE=AD+AE�Ϳ��Եó����ۣ�
��2�����������Եó���ADB=��CEA=90�㣬��1=��3������AB=AC�Ϳ��Եó���ADB�ա�CEA���Ϳ��Եó�BD=AE��AD=CE����AE=AD+DE�Ϳ��Եó�BD=CE+DE��
��� �⣺��1����ͼ�ף���BD��DE��CE��DE��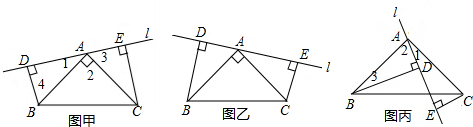
���D=��E=90�㣬
�ߡ�2=90�㣬
���1+��3=90�㣮
�ߡ�1+��4=90�㣬
���3=��4��
�ڡ�ADB�͡�CEA�У�
$\left\{\begin{array}{l}{��D=��E}\\{��4=��3}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��BD=AE��AD=CE��
��DE=AD+AE��
��DE=CE+BD��
��2��BD=DE+CE
���ɣ���ͼ����
��BD��DE��CE��DE��
���ADB=��CEA=90�㣮
���2+��3=90�㣮
�ߡ�1+��2=90�㣬
���3=��1��
�ڡ�ADB�͡�CEA�У�
$\left\{\begin{array}{l}{��ADB=��CEA}\\{��3=��1}\\{AB=CA}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��BD=AE��AD=CE��
��AE=AD+ED��
��BD=DE+CE��
���� ���⿼���˵���ֱ�������ε����ʵ����ã�ȫ�������ε��ж������ʵ����ã����ʱ֤��������ȫ���ǽ����Ĺؼ���


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
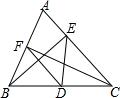 ��ͼ���ڡ�ABC�У�BE��AC�ڵ�E��CF��AB�ڵ�F��DΪBC�ߵ��е㣬����DE��DF��
��ͼ���ڡ�ABC�У�BE��AC�ڵ�E��CF��AB�ڵ�F��DΪBC�ߵ��е㣬����DE��DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�߶�a��ֱ��l��
��ͼ����֪�߶�a��ֱ��l���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
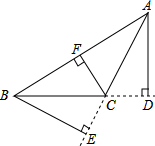 ��ͼ����ABC�У���ACB��90�㣬AD��BC��BE��AC��CF��AB������ֱ�ΪD��E��F�����߶�BE�ǡ�ABC��AC���ϵĸߣ�
��ͼ����ABC�У���ACB��90�㣬AD��BC��BE��AC��CF��AB������ֱ�ΪD��E��F�����߶�BE�ǡ�ABC��AC���ϵĸߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com