Question

1．若点M为正方形ABCD边AB上任意一点，作DM=MN交∠ABC外角的平分线于点N，求∠DMN的度数．

Answer 1

分析 首先过点N作NH⊥AB于点H，然后设正方形的边长为a，AM=x，NH=y；由DM=MN，利用勾股定理可证得AM=NH，继而证得Rt△ADM≌Rt△HMN（HL），然后由全等三角形的性质，求得∠ADM=∠HMN，继而求得∠DMN的度数．

解答 解：过点N作NH⊥AB于点H，
设正方形的边长为a，AM=x，NH=y；
∵四边形ABCD为正方形，且BN为外角平分线，
∴∠NBH=45°，故∠BNH=∠NBH=45°；
∴BH=NH=y，MH=a-x+y；
∵DM=MN，
∴DM²=MN²；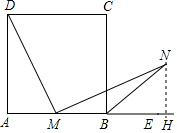
由勾股定理得：DM²=a²+x²，MN²=（a-x+y）²+y²，
故a²+x²=（a-x+y）²+y²，
∵（a-x+y）²+y²=（a-x）²+2（a-x）y+y²+y²
=a²-2ax+x²+2ay-2xy+2y²
=a²+x²-2（x-y）（a+y）
∴a²+x²=a²+x²-2（x-y）（a+y）
∴2（x-y）（a+y）=0，
∵a+y＞0，
∴x-y=0，x=y
∴AM=NH
在Rt△ADM与Rt△HMN中，
$\left\{\begin{array}{l}{AM=NH}\\{DM=MN}\end{array}\right.$，
∴Rt△ADM≌Rt△HMN（HL），
∴∠ADM=∠HMN；
∵∠ADM+∠AMD=90°，
∴∠HMN+∠AMD=90°，
∴∠DMN=180°-90°=90°．

点评 此题考查了正方形的性质、全等三角形的判定与性质以及勾股定理．注意准确作出辅助线是解此题的关键．