
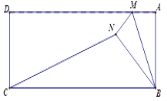
【题目】在一次数学探究活动课中,某同学有一块矩形纸片ABCD,已知AD=15,AB=9,M为线AD上的一个动点,将△ABM沿BM折叠得到△MBN,若△NBC是直角三角形,则AM长为__________.
【答案】3或27
【解析】
根据四边形ABCD为矩形以及折叠的性质得到∠A=∠MNB=90°,由M为AD上的一个动点可知若△NBC是直角三角形,∠NBC=90°与∠NCB=90°都不符合题意,只有∠BNC=90°.然后分 N在矩形ABCD内部与 N在矩形ABCD外部两种情况进行讨论,利用勾股定理求得结论即可.
解:∵四边形ABCD为矩形,
∴∠BAD=90°,
∵将△ABM沿BM折叠得到△MBN,
∴∠MAB=∠MNB=90°.
∵M为射线AD上的一个动点,△NBC是直角三角形,
∴∠NBC=90°与∠NCB=90°都不符合题意,
∴只有∠BNC=90°.
①当∠BNC=90°,N在矩形ABCD内部,如图1.
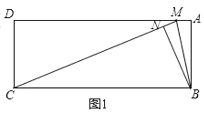
∵∠BNC=∠MNB=90°,
∴M、N、C三点共线,
∵AB=BN=9,BC=15,∠BNC=90°,
∴NC=12,
设AM=MN=x,则MD=15x,MC=12+x,
在Rt△MDC中,CD2+MD2=MC2,即92+(15x)2=(12+x)2,
解得x=3;
③当∠BNC=90°,N在矩形ABCD外部时,如图2.
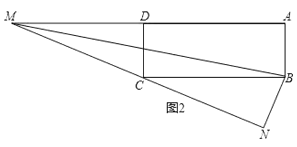
∵∠BNC=∠MNB=90°,
∴M、C、N三点共线,
∵AB=BN=9,BC=15,∠BNC=90°,
∴NC=12,
设AM=MN=y,则MD=y15,MC=y12,
在Rt△MDC中,CD2+MD2=MC2,即92+(y15)2=(y12)2,
解得y=27,
综上,AM的长为:3或27.
故答案为:3或27.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
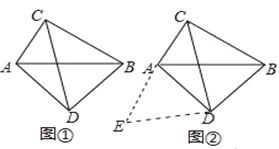
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图①中,若AC=2,BC=4,则CD= .
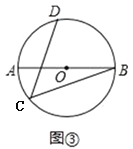
(2)如图③,AB是⊙O的直径,点C、D在⊙上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
拓展规律:
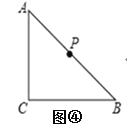
(3)如图4,△ABC中,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
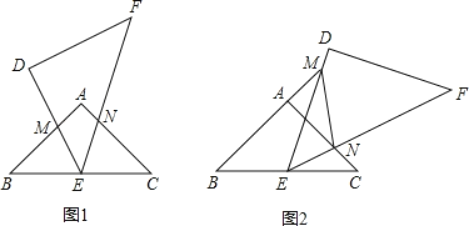
【题目】△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是 ,x与y的几组对应值列表如下:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | -1 | 0 | -1 | 0 |
| 3 | … |
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分并观察函数图象,写出该函数的两条性质.
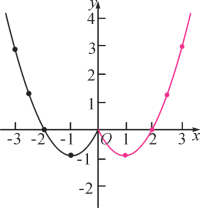
(3)进一步探究函数图象发现:关于x的方程2x2-4|x|=a有4个实数根,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:![]() (垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠
(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠![]() =20°.
=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
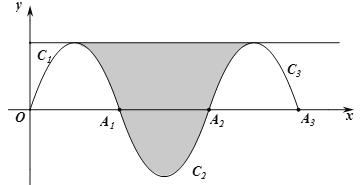
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于两点
轴交于两点![]() ,
,![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() .过抛物线
.过抛物线![]() ,
,![]() 顶点的直线与
顶点的直线与![]() ,
,![]() ,
,![]() 围成的如图中的阴影部分,那么该面积为_________.
围成的如图中的阴影部分,那么该面积为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com