
【题目】某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是 ,x与y的几组对应值列表如下:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | -1 | 0 | -1 | 0 |
| 3 | … |
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分并观察函数图象,写出该函数的两条性质.
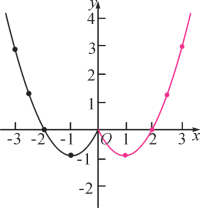
(3)进一步探究函数图象发现:关于x的方程2x2-4|x|=a有4个实数根,则a的取值范围是 .
【答案】(1)全体实数;(2)函数图象见解析;性质:①函数图象关于y轴对称;②当x>1时,y随x的增大而增大;(3)-2<a<0.
【解析】
(1)由函数解析式可判断自变量x的取值范围;
(2)根据表格中数据描点、画图即可;根据函数图象可直接得出其性质;
(3)方程2x2-4|x|=a有4个实数根,就是直线y=![]() 与y=x2-2|x|的图象有4个交点,,根据函数图象求解即可.
与y=x2-2|x|的图象有4个交点,,根据函数图象求解即可.
解:(1)由函数解析式可知,自变量x的取值范围是全体实数,
故答案为:全体实数;
(2)函数图象如图所示:
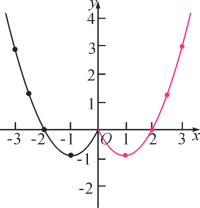
观察函数图象,可得出:
①函数图象关于y轴对称;
②当x>1时,y随x的增大而增大;
(3)方程2x2-4|x|=a可化简为x2-2|x|=![]() ,
,
方程2x2-4|x|=a有4个实数根时,即直线y=![]() 与y=x2-2|x|的图象有4个交点,
与y=x2-2|x|的图象有4个交点,
由函数图象可得:![]() 的取值范围是:-1<
的取值范围是:-1<![]() <0,
<0,
∴-2<a<0,
故答案为:-2<a<0.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
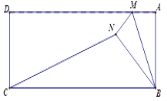
【题目】在一次数学探究活动课中,某同学有一块矩形纸片ABCD,已知AD=15,AB=9,M为线AD上的一个动点,将△ABM沿BM折叠得到△MBN,若△NBC是直角三角形,则AM长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
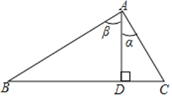
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinα=cosβ;③![]() ;④
;④![]() .其中正确的结论有____________.
.其中正确的结论有____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
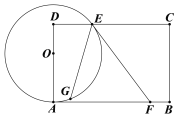
【题目】如图,O为矩形ABCD边AD上一点,以O为圆心,OA为半径画圆与CD交于点E,过点E作⊙O的切线EF交AB于F,点C关于EF的对称点G恰好落在⊙O上,若AD=4,AB=6,则OA的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
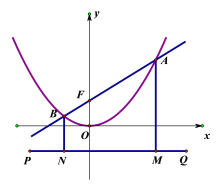
【题目】已知直线l:y=kx+4与抛物线y=![]() x2交于点A(x1,y1),B(x2,y2).
x2交于点A(x1,y1),B(x2,y2).
(1)求:![]() ;
;![]() 的值.
的值.
(2)过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.
(3)证明:![]() +
+![]() 为定值,并求出该值.
为定值,并求出该值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com