
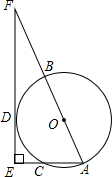
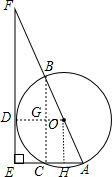
 如图,AB是⊙O的直径,AC为弦,D是
如图,AB是⊙O的直径,AC为弦,D是 |
| BC |
 |
| BC |
| 2 |
| 2 |
 |
| BC |
| OA2-AH2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| 4×3 |
| 1 |
| 2 |
5×
|
| 5×5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.
如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.查看答案和解析>>
科目:初中数学 来源: 题型:
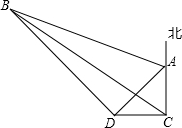 一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:
 将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.
将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com