
| A. | $\sqrt{8}$ | B. | $\sqrt{18}$ | C. | $\sqrt{56}$ | D. | $\sqrt{97}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{8}$被开方数含能开得尽方的因数或因式,故A错误;
B、$\sqrt{18}$被开方数含能开得尽方的因数或因式,故B错误;
C、$\sqrt{56}$被开方数含能开得尽方的因数或因式,故C错误;
D、$\sqrt{97}$被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
点评 本题考查最简二次根式的定义,根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 当直线与函数图象无交点时,m<0 | |
| B. | 当直线与函数图象只有1个交点时,m≥4 | |
| C. | 当直线与函数图象只有2个交点时,2≤m≤4 | |
| D. | 当直线与函数图象有三个交点时,0<m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
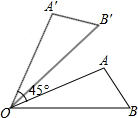 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com