练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．直角三角形的两条直角边长分别为16和12，则此三角形的外接圆半径是10，内切圆半径是4．

    分析 首先根据勾股定理求得该直角三角形的斜边是10，再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算．

    解答 解：由勾股定理可知：当两条直角边长分别为16和12，则直角三角形的斜边长=$\sqrt{1{6}^{2}+1{2}^{2}}$=20．
    根据直角三角形的外接圆的半径是斜边的一半，则其外接圆的半径是10；
    根据直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半，则其内切圆的半径是4．
    故答案为10，4．

    点评 此题要熟记直角三角形外接圆的半径和内切圆的半径公式：外接圆的半径等于斜边的一半；内切圆的半径等于两条直角边的和与斜边的差的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．如果x个人y天做了a个零件，那么y个人用相同的速度做x个零件需要的天数是（　　）
    A．$\frac{{x}^{2}}{a}$B．$\frac{a}{{x}^{2}}$C．$\frac{{a}^{2}}{x}$D．$\frac{x}{{a}^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某同学语文平时成绩得了70分，期中得了60分，平时成绩、期中成绩、期末成绩按15：15：70的比例计入总成绩，试问这位同学的语文期末考试至少必须得多少分，才能使总评成绩不低于70分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

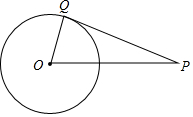    15．如图，点Q在⊙O上，分别根据下列条件，判定直线PQ与⊙O是否相切
    （1）OQ=6，OP=10，PQ=8
    （2）∠O=67.3°，∠P=22°42′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．下面一组按规律排列的数：0，2，8，26，80，…，则第2016个数是32015-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．计算：（-x）2•x3+（-x2）3=x5-x6．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如果点P（-1，3）在过原点的一直线上，那么这条直线的关系式是y=-3x，图象过二，四象限，且y随着x的增大而减小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

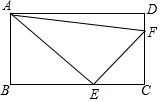    16．如图，在矩形ABCD中，AB=2，BC=3，AE是∠BAD的平分线，EF⊥AE，则AF的长为（　　）
    A．3$\sqrt{2}$B．4C．2$\sqrt{5}$D．$\sqrt{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知二次函数y=2x2-4x-6．
    （1）写出对称轴和顶点坐标；
    （2）在平面直角坐标系中，画出这个二次函数的图象；
    （3）当x取何值时，y＜0．

    查看答案和解析>>

    同步练习册答案