
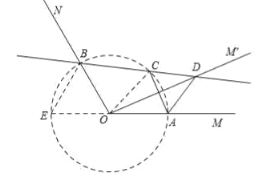
【题目】如图,已知![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,画直线
,画直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,有下列结论:
,有下列结论:
①![]() ; ②
; ②![]() 的大小随着
的大小随着![]() 的变化而变化;
的变化而变化;
③当![]() 时,四边形
时,四边形![]() 为菱形; ④
为菱形; ④![]() 面积的最大值为
面积的最大值为![]() ;
;

其中正确的是_____________.(把你认为正确结论的序号都填上).
【答案】①③④
【解析】
①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;
②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;
③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;
④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.
解:①∵A、C关于直线OM'对称,
∴OM'是AC的垂直平分线,
∴CD=AD,
故①正确;
②连接OC,由①知:OM'是AC的垂直平分线,
∴OC=OA,
∴OA=OB=OC,
以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,
则A、B、C都在⊙O上,
∵∠MON=120°,
∴∠BOE=60°,
∵OB=OE,
∴△OBE是等边三角形,
∴∠E=60°,
∵A、C、B、E四点共圆,
∴∠ACD=∠E=60°,
故②不正确;
③当α=30°时,即∠AOD=∠COD=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴∠OAC=60°,OC=OA=AC,
由①得:CD=AD,
∴∠CAD=∠ACD=∠CDA=60°,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴OC=OA=AD=CD,
∴四边形OADC为菱形,
故③正确;
④∵CD=AD,∠ACD=60°,
∴△ACD是等边三角形,
当AC最大时,△ACD的面积最大,
∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,
∴△ACD面积的最大值是:![]() AC2=
AC2=![]() ,
,
故④正确;
所以本题结论正确的有:①③④,
故答案为:①③④.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() .
.
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为动点,其对应的数为x,点P在-1到1之间运动时(即![]() ),请化简式子:
),请化简式子:![]() (写出化简过程);
(写出化简过程);
(3)在(1)、(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒一个单位长度的速度向左运动,同时点B以每秒2个单位长度,点C以每秒5个单位长度的速度向右运动3秒钟后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请求BC-AB的值.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:

(1)分别在射线OA、OC上截取线段OD、OE,且OE=2OD;
(2)连接DE;
(3)以O为顶点,画∠DOF=∠EDO,射线OF交DE于点F;
(4)写出图中∠EOF的所有余角: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的分式方程![]() ①和一元二次方程
①和一元二次方程![]() ②中,m为常数,方程①的根为非负数.
②中,m为常数,方程①的根为非负数.
(1)求m的取值范围;
(2)若方程②有两个整数根x1、x2,且m为整数,求方程②的整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法计算:
(1)0.36+(-7.4)+0.5+(-0.6)+0.14;
(2)(-2.125)+![]() +(-3.2);
+(-3.2);
(3)![]() .
.
(4)|-0.75|+(-3)-(-0.25)+![]() .
.
(5)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①8+(﹣10)+(﹣2)﹣(﹣5)
②2![]() ﹣3
﹣3![]() ﹣5
﹣5![]() ﹣|﹣3
﹣|﹣3![]() |
|
③(﹣1![]() )+1.25+(﹣8.5)+10
)+1.25+(﹣8.5)+10![]()
④(![]() )×(﹣12)
)×(﹣12)
⑤(﹣199![]() )×5(用简便方法计算)
)×5(用简便方法计算)
⑥10×(﹣![]() )﹣2×
)﹣2×![]() +(﹣3)×(﹣
+(﹣3)×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某司机在东西路上开车接送乘客,他早晨从A地出发,(去向东的方向正方向),到晚上送走最后一位客人为止,他一天行驶的的里程记录如下(单位:㎞)
+10 ,— 5, —15 ,+ 30 ,—20 ,—16 ,+ 14
(1) 若该车每百公里耗油 3 L ,则这车今天共耗油 多少升?
(2) 据记录的情况,你能否知道该车送完最后一个乘客是,他在A地的什么方向?距A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了 名学生,请补全条形统计图;
(2)被调查同学中恰好有5名学来自初一12班,其中有2名同学选择了篮球,有3名同学选择了乒乓球,曹老师打算从这5名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好为一人选择篮球、一人选择乒乓球的概率.
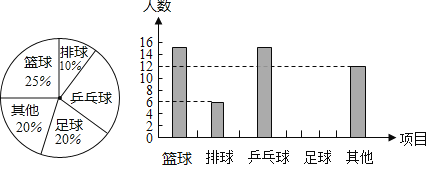
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com