
分析 (1)依据$\sqrt{{a}^{2}}$=a(a≥0),进行化简即可;
(2)将$\sqrt{\frac{8}{5}}$变形为$\frac{2\sqrt{2}}{\sqrt{5}}$,然后再进行分母有理化即可;
(3)进行分母有理化即可;
(4)先将原式变形为$\frac{y\sqrt{3y}}{x\sqrt{2}}$,然后再进行分母有理化即可.
解答 解:(1)$\sqrt{8{a}^{2}{b}^{3}}$=$\sqrt{4{a}^{2}{b}^{2}•2b}$=2ab$\sqrt{2b}$;
(2)$\sqrt{\frac{8}{5}}$=$\frac{2\sqrt{2}}{\sqrt{5}}$=$\frac{2\sqrt{2}×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{2\sqrt{10}}{5}$;
(3)$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{6}}{3}$;
(4)$\sqrt{\frac{3{y}^{3}}{2{x}^{2}}}$=$\frac{y\sqrt{3y}}{x\sqrt{2}}$=$\frac{y\sqrt{6y}}{2x}$.
点评 本题主要考查的是二次根式的性质与化简,掌握二次根式的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
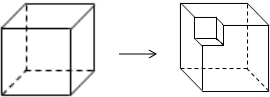 如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )
如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )| A. | 27cm3,54cm2 | B. | 26cm3,54cm2 | C. | 27cm3,51cm2 | D. | 26cm3,51cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com