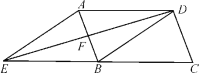
【题目】如图，在平行四边形ABCD中，DB＝DA，∠ADB的平分线交AB于点F，交CB的延长线于点E，连接AE.
(1)求证：四边形AEBD是菱形；
(2)若DC＝
，EF：BF＝3，求菱形AEBD的面积．
【答案】（1）见解析；（2）15.
【解析】
（1）由△AFD≌△BFE，推出AD=BE，可知四边形AEBD是平行四边形，再根据DB＝DA可得结论；
（2）先求出BF的长，再求出EF的长即可解决问题.
（1）证明：∵四边形ABCD是平行四边形，
∴AD∥CE，
∴∠DAF=∠EBF，
∵∠AFD=∠EFB，AF=FB，
∴△AFD≌△BFE，
∴AD=EB，∵AD∥EB，
∴四边形AEBD是平行四边形，
∵BD=AD，
∴四边形AEBD是菱形．
（2）∵四边形ABCD是平行四边形，
∴CD=AB=
，
∵四边形AEBD是菱形，
∴AB⊥DE，AF=FB=
，
∵EF：BF＝3
∴EF=
∴DE=2EF=
∴S菱形AEBD=
ABDE=××3=15．
科目：初中数学 来源： 题型：
【题目】已知反比例函数
（k为常数，k≠0）的图象经过点A（2，3）．
（1）求这个函数的解析式；
（2）判断点B（－1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当－3＜x＜－1时，求y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
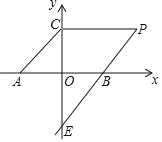
【题目】如图，直线y＝x+3与x轴、y轴分别相交于A、C两点，过点B（6，0），E（0，﹣6）的直线上有一点P，满足∠PCA＝135°．
（1）求证：四边形ACPB是平行四边形；
（2）求直线BE的解析式及点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知代数式
，当
时，该代数式的值为3．
（1）求c的值；
（2）已知：当
时，该代数式的值为0.
①求：当
时，该代数式的值；
②若
，
，
，试比较a与d的大小，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（ ）
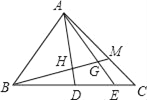
A. 3：2：1 B. 5：3：1 C. 25：12：5 D. 51：24：10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列事件中是不可能事件的是（ ）
A. 任意画一个四边形，它的内角和是
B. 若
，则
C. 一只不透明的袋子共装有3个小球，它们的标号分别为1、2、3，从中摸出一个小球，标号是“5”
D. 掷一枚质地均匀的硬币，落地时正面朝上
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着人民生活水平的提高，汽车进入家庭的越来越多．我市某小区在2007年底拥有家庭轿车64辆，到了2009年底，家庭轿车数为100辆．
（1）若平均每年轿车数的增长率相同，求这个增长率．
（2）为了缓解停车矛盾，多增加一些车位，该小区决定投资15万元，再造一些停车位．据测算，建造一个室内停车位，需5000元；建造一个室外停车位，需1000元．按实际情况考虑，计划室外停车位数不少于室内车位的2倍，又不能超过室内车位的2.5倍．问，该小区有哪几种建造方案？应选择哪种方案最合理？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在直角坐标平面内，直线y=
x+2分别与x轴、y轴交于点A、C．抛物线y=﹣
+bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．
（1）求上述抛物线的表达式；
（2）联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；
（3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，有下列条件：①AB
CD；②ADBC；③AC=BD；④AC⊥BD．
（1）从中任选一个作为已知条件，能判定四边形ABCD是平行四边形的概率是 ．
（2）从中任选两个作为已知条件，请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率，并判断四边形ABCD是菱形的概率？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com