

分析 (1)连接BC,根据圆周角定理得到BC是⊙A的直径,根据勾股定理计算即可求出点B的坐标;
(2)过点P作PD⊥x轴于点D,根据正切的定义求出∠OBC的度数,根据锐角三角函数的定义求出PD、OD,得到点P的坐标;
(3)根据切线长定理求出∠EPB=60°,证明PE∥OD,求出切点E的坐标.
解答 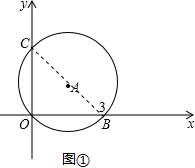 解:(1)如图①,连接BC,
解:(1)如图①,连接BC,
∵∠BOC=90°,
∴BC是⊙A的直径,
∴$BC=2\sqrt{3}$,
∵$C({0,\sqrt{3}})$,
∴$OC=\sqrt{3}$.
∴OB=$\sqrt{B{C}^{2}-O{C}^{2}}$=3,
∴B(3,0);
(2)如图②,过点P作PD⊥x轴于点D,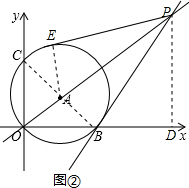
∵PB为⊙A的切线,
$C({0,\sqrt{3}})$,
∴$tan∠OBC=\frac{OC}{OB}=\frac{{\sqrt{3}}}{3}$.
∴∠OBC=30°,
∴∠AOB=30°.
∴∠OPB=180°-∠POB-∠ABO-∠ABP=30°.
∴OB=BP=3,
在Rt△PBD中,∠PDB=90°,∠PBD=60°,BP=3,
∴$BD=\frac{3}{2}$,$PD=\frac{3}{2}\sqrt{3}$.
∵OB=3,
∴$OD=OB+BD=\frac{9}{2}$.
∴$P({\frac{9}{2},\frac{3}{2}\sqrt{3}})$;
(3)由(2)得,∠OPB=30°,
∵PE、PB是⊙A的切线,
∴∠EPA=∠OPB=30°,
∴∠EPB=60°,又∠PBD=60°,
∴PE∥OD,
∴$E({\frac{3}{2},\frac{3}{2}\sqrt{3}})$.
点评 本题考查的是圆的知识的综合运用,掌握圆周角定理、切线的性质定理以及锐角三角函数的定义是解题的关键,解答时,注意辅助线的作法和勾股定理的正确运用.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
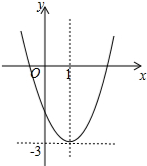 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
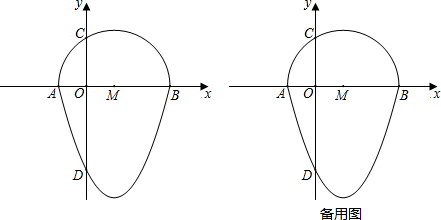
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com