
如图,已知抛物线经过点 A(﹣1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
点 M 是线段 BC 上的点(不与 B,C 重合),过 M 作 MN∥y 轴交抛物线于 N,若点 M 的横坐标为
m,请用 m 的代数式表示 MN 的长.
(3)在的条件下,连接 NB、NC,是否存在 m,使△BNC 的面积最大?若存在,求 m 的值;若不 存在,说明理由.

【考点】二次函数综合题.
【专题】压轴题;数形结合.
【分析】(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式. 先利用待定系数法求出直线 BC 的解析式,已知点 M 的横坐标,代入直线 BC、抛物线的解析式中, 可得到 M、N 点的坐标,N、M 纵坐标的差的绝对值即为 MN 的长.
(3)设 MN 交 x 轴于 D,那么△BNC 的面积可表示为:S△BNC=S△MNC+S△MNB=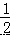 MN(OD+DB)
MN(OD+DB)
= 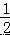 MN•OB,MN 的表达式在中已求得,OB 的长易知,由此列出关于 S△BNC、m 的函数关系式, 根据函数的性质即可判断出△BNC 是否具有最大值.
MN•OB,MN 的表达式在中已求得,OB 的长易知,由此列出关于 S△BNC、m 的函数关系式, 根据函数的性质即可判断出△BNC 是否具有最大值.
【解答】解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3. 设直线 BC 的解析式为:y=kx+b,则有:
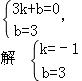 ;
;
故直线 BC 的解析式:y=﹣x+3.
已知点 M 的横坐标为 m,MN∥y,则 M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故 MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
(3)如图;


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
.如图,直线 y=kx+b 交坐标轴于 A(﹣2,0)、B(0,3)两点,则不等式 kx+b>0 的解集是( )
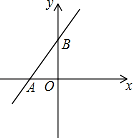
A.x>﹣2 B.x>3 C.x<﹣2 D.x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
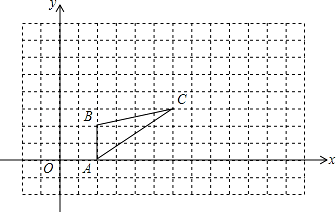
如图,图中的小方格都是边长为 1 的正方形,△ABC 的 A、B、C 三点坐标为 A、B、C(6,3).
(1)请在图中画出一个△A′B′C′,使△A′B′C′与△ABC 是以坐标原点为位似中心,相似比为 2 的位 似图形.
求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
运用等式性质进行的变形,正确的是( )
A.如果 a=b,那么 a+2=b+3 B.如果 a=b,那么 ac=bc C.如果 a=b,那么 D.如果 a2=3a,那么 a=3
D.如果 a2=3a,那么 a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场销售一种西装和领带,西装每套定价 1000 元,领带每条定价 200 元.“国庆节”期间商场 决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带; 方案二:西装和领带都按定价的 90%付款. 现某客户要到该商场购买西装 20 套,领带 x 条(x>20).
(1)若该客户按方案一购买,需付款 元.(用含 x 的代数式表示)若该客户按方案 二购买,需付款 元.(用含 x 的代数式表示)
若 x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当 x=30 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com