练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图，把一副常用的三角板如图所示拼在一起，那么图中∠ABF=15°．

    分析 根据常用的三角板的特点求出∠EAD和∠BFD的度数，根据三角形的外角的性质计算即可．

    解答 解：由一副常用的三角板的特点可知，∠EAD=45°，∠BFD=30°，
    ∴∠ABF=∠EAD-∠BFD=15°，
    故答案为：15°．

    点评 本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．如果3、5、a是一个三角形的三边，那么a的取值范围是2＜a＜8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）解不等式组$\left\{\begin{array}{l}{\frac{2}{3}x+5＞1-x}\\{x-1＜\frac{3}{4}x-\frac{1}{8}}\end{array}\right.$，并写出它的非负整数解．
    （2）解不等式组$\left\{\begin{array}{l}{x-3（x-2）≤4}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$，并把解集表示在数轴上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

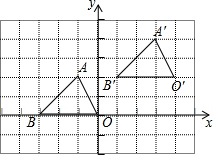    12．如图，△A′B′O′是由△ABO平移得到的，点A的坐标为（-1，2），它的对应点A′的坐标为（3，4），△ABO内仼意点P（a，b）平移后的对应点P′的坐标为（　　）
    A．（a，b）B．（-a，-b）C．（a+2，b+4）D．（a+4，b+2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    ①（$\sqrt{5}$+2）（$\sqrt{5}$-2）+（$\frac{1}{2}$）-2-$\sqrt{25}$       
    ②$\sqrt{12}（\sqrt{75}+3\sqrt{\frac{1}{3}}-\sqrt{48}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．函数y=$\sqrt{x-2}$+1中，自变量x的取值范围是（　　）
    A．x＞2B．x＜2C．x≥2D．x≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，四边形ABCD为正方形，△BPC为等边三角形，连接PD、BD，则∠BDP=30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若一个扇形的半径为3cm，圆心角为60°，现将此扇形围成一个圆锥的侧面，则这个圆锥的底面积为$\frac{1}{4}$πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

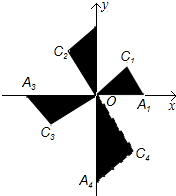    14．在平面直角坐标系xOy中，Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3…=30°，若点A1的坐标（3，0），OA1=OC2，OA2=OC3，OA3=OC4…则依此规律OA2016的长为（　　）
    A．3×（$\frac{3}{2}$$\sqrt{3}$）2013B．3×（$\frac{3}{2}\sqrt{3}$）2014C．3×（$\frac{3\sqrt{3}}{2}$）2015D．3×（$\frac{3\sqrt{3}}{2}$）2016

    查看答案和解析>>

    同步练习册答案