
【题目】已知二次函数的图象以![]() 为顶点,且过点
为顶点,且过点![]()
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
【答案】(1)![]() ;(2)该函数的图像与坐标轴的交点是
;(2)该函数的图像与坐标轴的交点是![]() ,
,![]() ,
,![]()
【解析】
(1)根据图象的顶点A(1,4)来设该二次函数的关系式,然后将点B代入,即用待定系数法来求二次函数解析式;
(2)令y=0,然后将其代入函数关系式,解一元二次方程即可,再令x=0,求出与y轴交点.
(1)由顶点A(1,4),可设二次函数关系式为y=a(x+1)2+4(a≠0).
∵二次函数的图象过点B(2,5),
∴点B(2,5)满足二次函数关系式,
∴5=a(2+1)2+4,
解得a=1.
∴二次函数的关系式是y=(x+1)2+4;
(2)令x=0,则y=(0+1)2+4=3,
∴图象与y轴的交点坐标为(0,3);
令y=0,则0=(x+1)2+4,
解得x1=3,x2=1,
故图象与x轴的交点坐标是(3,0)、(1,0).
答:图象与y轴的交点坐标为(0,3),与x轴的交点坐标是(3,0)、(1,0).


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
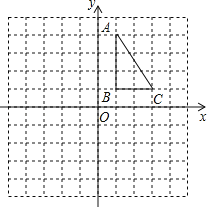
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
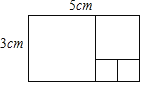
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
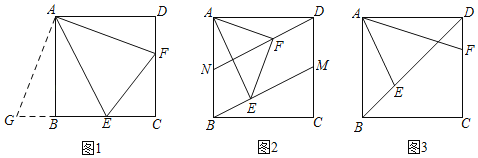
【题目】已知,正方形ABCD,∠EAF=45°,
(1)如图1,当点E,F分别在边BC,CD上,连接EF,求证:EF=BE+DF;
(2)如图2,点M,N分别在边AB,CD上,且BN=DM,当点E,F分别在BM,DN上,连接EF,请探究线段EF,BE,DF之间满足的数量关系,并加以证明;
(3)如图3,当点E,F分别在对角线BD,边CD上,若FC=2,则BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
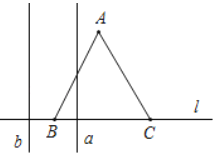
【题目】如图,边长为![]() 的正
的正![]() 的边
的边![]() 在直线
在直线![]() 上,两条距离为
上,两条距离为![]() 的平行直线
的平行直线![]() 和
和![]() 垂直于直线
垂直于直线![]() ,
,![]() 和
和![]() 同时向右移动(
同时向右移动(![]() 的起始位置在
的起始位置在![]() 点),速度均为每秒
点),速度均为每秒![]() 个单位,运动时间为
个单位,运动时间为![]() (秒),直到
(秒),直到![]() 到达
到达![]() 点停止,在
点停止,在![]() 和
和![]() 向右移动的过程中,记
向右移动的过程中,记![]() 夹在
夹在![]() 和
和![]() 间的部分的面积为
间的部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.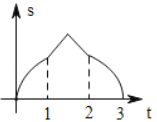 B.
B.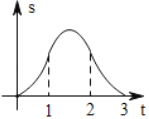
C.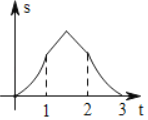 D.
D.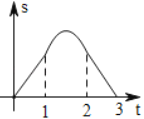
查看答案和解析>>
科目:初中数学 来源: 题型:
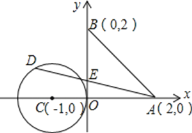
【题目】如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E ,则△ABE面积的最小值是 _____
查看答案和解析>>
科目:初中数学 来源: 题型:
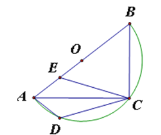
【题目】如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆.点D在弧![]() 上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:①若∠ACE=20°,则∠BAC=25°;②若BC=3,AC=4,则
上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:①若∠ACE=20°,则∠BAC=25°;②若BC=3,AC=4,则![]() ;给出下列判断,正确的是( )
;给出下列判断,正确的是( )
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若抛物线![]() 与抛物线
与抛物线![]() 的开口大小相同,方向相反,且抛物线
的开口大小相同,方向相反,且抛物线![]() 经过
经过![]() 的顶点,我们称抛物线
的顶点,我们称抛物线![]() 为
为![]() 的“友好抛物线”.
的“友好抛物线”.
(1)若![]() 的表达式为
的表达式为![]() ,求
,求![]() 的“友好抛物线”的表达式;
的“友好抛物线”的表达式;
(2)已知抛物线![]() 为
为![]() 的“友好抛物线”.求证:抛物线
的“友好抛物线”.求证:抛物线![]() 也是
也是![]() 的“友好抛物线”;
的“友好抛物线”;
(3)平面上有点![]() ,
,![]() ,抛物线
,抛物线![]() 为
为![]() 的“友好抛物线”,且抛物线
的“友好抛物线”,且抛物线![]() 的顶点在第一象限,纵坐标为2,当抛物线
的顶点在第一象限,纵坐标为2,当抛物线![]() 与线段
与线段![]() 没有公共点时,求
没有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com