
【题目】如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边分别与坐标轴交于点A和点B,则OA+OB的值为________.

【答案】8
【解析】
过P点作PM⊥x轴于M点,PN⊥y轴于N点,先证明出△PBN≌△PAM,然后得到BN=AM,进而可以得到OA+OB=OM+AM+OB=OM+OB+BN=OM+ON=8.
如图,过P点作PM⊥x轴于M点,PN⊥y轴于N点,
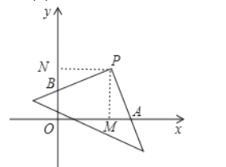
则∠PNB=∠PMA=90°,∠NPM=90°,
∵∠BPA=90°,
∴∠NPB=∠MPA=90°-∠BPM,
∵P(4,4)
∴PM=PN=OM=ON=4
在△PBN和△PAM中,
∠NPB=∠MPA,PN=PM,∠PNB=∠PMA
∴△PBN≌△PAM.
∴PB=PA,BN=AM
∴OA+OB=OM+AM+OB=OM+BN+ON=OM+ON=4+4=8.
故填8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,根据要求回答下列问题:
(1)点A关于y轴对称点A′的坐标是 ;点B关于y轴对称点B′的坐标是
(2)作出△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,AD为中线,点P是AD上一点,点Q是AC上一点,且∠BPQ+∠BAQ=180°.
(1)若∠ABP=α,求∠PQC的度数(用含α的式子表示);
(2)求证:BP=PQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
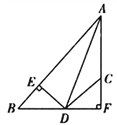
【题目】如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.
(1)图中与△BDE全等的三角形是 ,请加以证明;
(2)若AE=6 cm,AC=4 cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
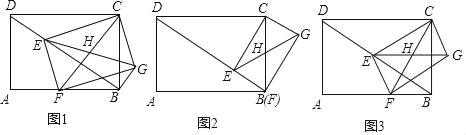
【题目】如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.
(1)①如图2,当点F与点B重合时,CE= ,CG= ;
②如图3,当点E是BD中点时,CE= ,CG= ;
(2)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明;
(3)在图1,![]() 的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
(4)在图1,设DE的长为x,矩形CEFG的面积为S,试求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后回答问题:
在关于x的一元二次方程ax2+bx+c=0(a≠0)中,若各项的系数之和为零,即a+b+c=0,则有一根为1,另一根为![]() .
.
证明:设方程的两根为x1,x2,由a+b+c=0,知b=-(a+c),
∵x=![]() =
=![]() ,
,
∴x1=1,x2=![]() .
.
(1)若一元二次方程ax2+bx+c=0(a≠0)的各项系数满足a-b+c=0,请直接写出此方程的两根;
(2)已知方程(ac-bc)x2+(bc-ab)x+(ab-ac)=0有两个相等的实数根,运用上述结论证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分线.其中正确的是= _________ .(写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com