Question

5．如图所示，将△ABC沿着DE翻折，点B与点B′对应．图（1）中点B′在∠ABC内部，图（2）中点B′在∠ABC外部，请分别写出∠1、∠2与∠B的数量关系，并说明理由．

Answer 1

分析 ①根据折叠性质得出∠BED=∠B′ED，∠BDE=∠B′DE，根据三角形内角和定理得出∠BED+∠BDE=180°-∠B，代入∠1+∠2=180°+180°-2（∠BED+∠BDE）求出即可；
②由图形翻折变换的性质可得到∠B=∠B′，再根据∠2=∠EB′B+∠EBB′即可求出答案．

解答 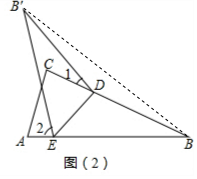解：①如图（1），2∠B=∠1+∠2，
理由是：∵延DE折叠B和B′重合，
∴∠BED=∠B′ED，∠BDE=∠B′DE，
∵∠BED+∠BDE=180°-∠B，∠1+∠2=180°+180°-2（∠BED+∠BDE），
∴∠1+∠2=360°-2（180°-∠B）=2∠B；
如图（2）由图形翻折变换的性质可知，∠B=∠B′，
连接BB′，
则∠2=∠EB′B+∠EBB′
=∠DB′E+∠DB′B+∠DBE+∠B′BD，
=2∠B+∠DB′B+∠B′BD
=2∠B+∠1即∠2-∠1=2∠B．

点评 此题考查了折叠的性质，三角形外角性质，三角形内角和定理的应用，主要考查学生运用定理进行推理和计算的能力．