
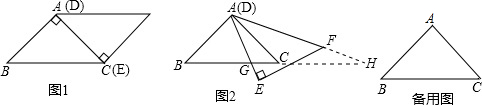
���� ��1�����ݡ�ABC���EFDΪ����ֱ�������Σ�AC��DE�غϣ��������������ε��ж��������ɵó����ۣ��ɡ�AGB�ǡ�AGC�͡�AGH����ǣ����ǵõ���GAC=��H����ACB=��GAH=45�㣬���ǵõ����ۣ�
��2���ɡ�AGC�ס�HAB���������Ӧ�߳ɱ����г�����x��y�Ĺ�ϵʽ��9��y=x��9������⣻
��3������Ҫ���÷������۵�˼�룬��CG��$\frac{1}{2}$BCʱ����CG=$\frac{1}{2}$BCʱ����CG��$\frac{1}{2}$BCʱ�ֱ�ó����ɣ�
��� �⣺��1�������ƣ�
���ɣ��ߡ�ABC���EFDΪ����ֱ�������Σ�AC��DE�غϣ�
�ߡ�H+��HAC=45�㣬��HAC+��CAG=45�㣬
���H=��CAG��
�ߡ�ACG=��B=45�㣬
���AGC�ס�HAB��
�ڡ�AGC�ס�HAB��
���ɣ��ߡ�AGB�ǡ�AGC�͡�AGH����ǣ�
���AGB=��GAC+��ACB��
��AGB=��GAH+��H��
�ߡ�ACB=��GAH=45�㣬
���GAC=��H��
���AGC�ס�HGA��
��2���ߡ�AGC�ס�HAB��
��AC��HB=GC��AB����9��y=x��9��
��y=$\frac{81}{x}$��
��AB=AC=9����BAC=90�㣬
��BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{9}^{2}+{9}^{2}}$=9$\sqrt{2}$��
��y����x�ĺ�����ϵʽΪy=$\frac{81}{x}$��0��x��9$\sqrt{2}$����
��3���ٵ�CG��$\frac{1}{2}$BCʱ����GAC=��H����HAC��
��AC��CH��
��AG��AC��
��AG��CH��GH��
�֡�AH��AG��AH��GH��
��ʱ����AGH�������ǵ��������Σ�
�ڵ�CG=$\frac{1}{2}$BCʱ��GΪBC���е㣬H��C�غϣ���AGH�ǵ��������Σ�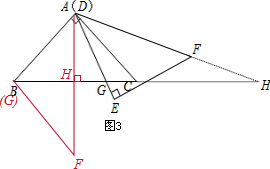
��ʱ��GC=$\frac{9\sqrt{2}}{2}$����x=$\frac{9\sqrt{2}}{2}$��
�۵�CG��$\frac{1}{2}$BCʱ���ɣ�1����AGC�ס�HGA��
����AGH���ǵ��������Σ�ֻ���ܴ���GH=AH����GH=AH����AC=CG����ʱx=9��
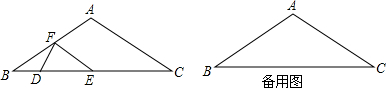
��ͼ3����CG=BCʱ��
ע�⣺DF����ת����BC��ֱ��λ�ã�
��ʱB��E��G�غϣ���AGH=��GAH=45�㣬
���AGH��������������CG=9$\sqrt{2}$��
������������x=9��x=$\frac{9\sqrt{2}}{2}$��9$\sqrt{2}$ʱ����AGH�ǵ��������Σ�
���� ������Ҫ����ѧ�������������ε��ж������ʣ����������ε����ʣ�����ֱ�������ε����ʣ���ת�����ʵ�֪ʶ�����������գ��ۺ��Խ�ǿ�����׳̶����У���һ���ܵ��͵���Ŀ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{2}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com