
【题目】如图,已知AB是⊙O的直径,C,D为⊙O上的点且∠ABC=∠DBC,过C作CE⊥BD交BD的延长线于点E.
(1)求证:CE是⊙O的切线.
(2)若F是OB的中点,FG⊥OB交CE于点G,FG=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
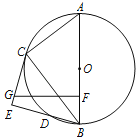
【答案】(1)证明见解析;(2)⊙O的半径=4
【解析】
(1)连接OC,根据等腰三角形的性质得到∠OCB=∠OBC,推出OC∥BE,得到OC⊥CE,根据切线的判定定理得到CE是⊙O的切线;
(2)延长EC,BA相交于R,根据余角的性质得到∠ACR=∠ABC,根据相似三角形的性质得到![]() ,设AR=3x,RC=4x,设⊙O的半径为2a,根据勾股定理和相似三角形的性质即可得到结论.
,设AR=3x,RC=4x,设⊙O的半径为2a,根据勾股定理和相似三角形的性质即可得到结论.
解:(1)连接OC,∵OC=OB,
∴∠OCB=∠OBC,
∵∠ABC=∠DBC,
∴OC∥BE,
∵CE⊥BD,
∴OC⊥CE,
∴CE是⊙O的切线;
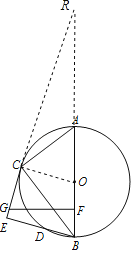
(2)延长EC,BA相交于R,
∵∠ACR+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACR=∠ABC,
∴△ACR∽△CBR,
∴![]() ,
,
设AR=3x,RC=4x,
设⊙O的半径为2a,
4a2+16x2=(3x+2a)2,x=![]() a,
a,
∵△OCR∽△GFR
∴![]() ,
,
∴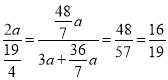 ,
,
∴a=2,
∴⊙O的半径=4.


科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们可以用![]() 表示a,b两数中较大的数,例如
表示a,b两数中较大的数,例如![]() ,
,![]() .类似的若函数y1、y2都是x的函数,则y=min{y1,y2}表示函数y1和y2的取小函数.
.类似的若函数y1、y2都是x的函数,则y=min{y1,y2}表示函数y1和y2的取小函数.
(1)设![]() ,
,![]() ,则函数
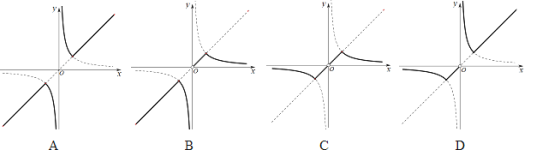
,则函数![]() 的图像应该是___________中的实线部分.
的图像应该是___________中的实线部分.
(2)请在下图中用粗实线描出函数![]() 的图像,观察图像可知当x的取值范围是_____________________时,y随x的增大而减小.
的图像,观察图像可知当x的取值范围是_____________________时,y随x的增大而减小.
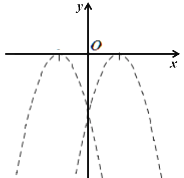
(3)若关于x的方程![]() 有四个不相等的实数根,则t的取值范围是_____________________.
有四个不相等的实数根,则t的取值范围是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 是射线
是射线![]() 上一个动点(不与点
上一个动点(不与点![]() 、
、![]() 重合),联结
重合),联结![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
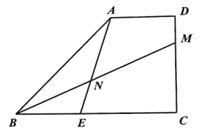
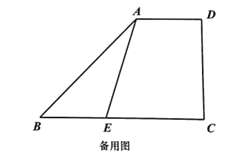
(1)求![]() 的长;
的长;
(2)当动点![]() 在线段
在线段![]() 上时,试求
上时,试求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域;
之间的函数解析式,并写出函数的定义域;
(3)当动点![]() 运动时,直线
运动时,直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() ,请直接写出这时线段
,请直接写出这时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c图象如图所示,则下列结论中正确的个数( )
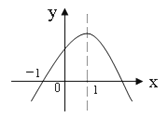
① abc<0;② a-b+c<0;③ a+b+c>0;④ 2c =3b
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
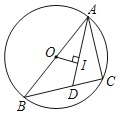
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则sin∠CAD的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
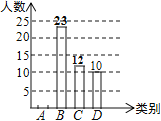
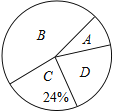
表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)这次共抽取_________名学生进行统计调查,扇形统计图中,![]() 类所对应的扇形圆心角的大小为__________
类所对应的扇形圆心角的大小为__________
(2)将条形统计图补充完整
(3)该校共有1500名学生,估计该校表示“喜欢”的![]() 类的学生大约有多少人?
类的学生大约有多少人?
各类学生人数条形统计图各类学生人数扇形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
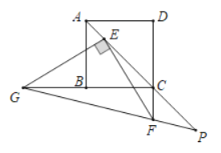
【题目】如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com