
【题目】等边![]() 的边长为3,在边
的边长为3,在边![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为一边作等边
为一边作等边![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
【答案】2或![]()
【解析】
分两种情况:①当C1在A1B的上方时,证明△A1BC≌△ABC1,则A1C=AC1=2;②当C1在A1B的下方时,作辅助线,构建全等三角形和直角三角形,同理得:△ABA1≌△CBC1,则C1C=A1A=1,∠C1CB=∠BAC=60°,得到30°的Rt△C1CD,根据性质求得CD=![]() ,C1D=
,C1D=![]() ,最后利用勾股定理可得结论.
,最后利用勾股定理可得结论.
分两种情况:
① 当C1在A1B的上方时,如图1,
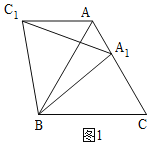
∵AB=3,AA1=2,
∴A1C=3-1=2,
∵△ABC和△A1BC1是等边三角形,
∴AB=BC,A1B=BC1,∠ABC=∠A1BC1=60°,
∴∠A1BC=∠ABC1,
在△A1BC和△ABC1中,
∵BC=AB,∠A1BC=∠C1BA,A1B=C1B,
∴△A1BC≌△ABC1(SAS),
∴A1C=AC1=2;
② 当C1在A1B的下方时,如图2,连接C1C,过C1作C1D⊥AC于D,
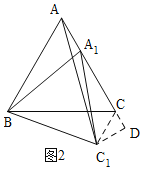
同理得:△ABA1≌△CBC1,
∴C1C=A1A=1,∠C1CB=∠BAC=60°,
∵∠ACB=60°,
∴∠C1CD=60°,
Rt△C1CD中,∠CC1D=30°,
∴CD=![]() C1C=
C1C=![]() ,C1D=
,C1D=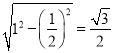 ,
,
Rt△AC1D中,AD=3+![]() =
=![]() ,
,
由勾股定理得:AC1=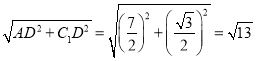 ,
,
综上所述,则线段A1C的长为2或![]() .
.
故答案为:2或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9![]() 与7
与7![]() ,则斜边BC的长为( )
,则斜边BC的长为( )
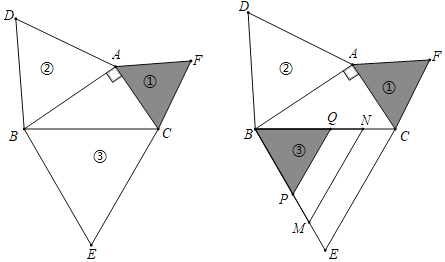
A.5B.9C.10D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是 (填A或B).
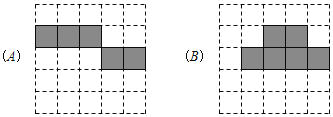
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)

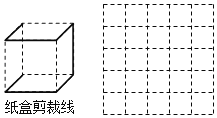
(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数![]()
![]() x
x![]() 的图象上任意一点,PA
的图象上任意一点,PA![]() x轴于点A,PD
x轴于点A,PD![]() y轴于点D,分别交反比例函数
y轴于点D,分别交反比例函数![]()
![]() x
x![]() ,
,![]() k
k![]() 的图象于点B,C
的图象于点B,C![]() 下列结论:①当k
下列结论:①当k![]() 时,BC是
时,BC是![]() PAD的中位线;②不论k为何值,都有
PAD的中位线;②不论k为何值,都有![]() PDA∽
PDA∽![]() PCB;③当四边形ABCD的面积等于2时,k
PCB;③当四边形ABCD的面积等于2时,k![]() ④若点P
④若点P![]() ,将
,将![]() PCB沿CB对折,使得P点恰好落在OA上时,则
PCB沿CB对折,使得P点恰好落在OA上时,则![]() ;其中正确的个数有( )
;其中正确的个数有( )
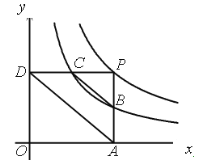
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件,如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若在销售过程中每一件商品有a(a>1)元的其他费用,商家发现当售价每件不低于57元时,每月的销售利润随x的增大而减小,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.

(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com