
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,点
的直径,点![]() 是半圆
是半圆![]() 的中点,点
的中点,点![]() 是
是![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() 交
交![]() 于点
于点![]() .
.
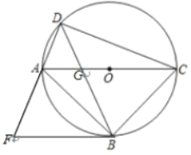
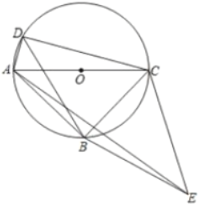
图1 图2
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,求证:
,求证:![]() 与
与![]() 相切;
相切;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,把![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,当点
,当点![]() 在
在![]() 运动时,探究线段
运动时,探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 与点
与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 之间的数量关系和位置关系分别是 .
之间的数量关系和位置关系分别是 .
(2)深入探究
如图②,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 在直线
在直线![]() 上,对角线
上,对角线![]() 所在的直线交直线
所在的直线交直线![]() 于点
于点![]() ,则线段
,则线段![]() 之间有什么数量关系?请仅就图②给出证明.
之间有什么数量关系?请仅就图②给出证明.
(3)拓展思维
如图②,若点![]() 在直线
在直线![]() 上,且线段
上,且线段![]() ,当
,当![]() 时,直接写出此时正方形
时,直接写出此时正方形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,口罩供不应求.某口罩企业为指导生产,在二月份期间对甲乙丙丁四条生产线日产量进行调研,根据调研数据,绘制出如下两幅不完整的统计图.观察统计图,请解答以下问题:
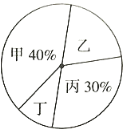
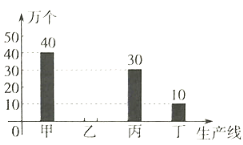
(1)求二月份该企业口罩单日产量(二月份计![]() 天).
天).
(2)求乙条生产线单日产量是多少,并补全频数分布直方图.
(3)为满足市场需求,该公司改进生产技术,使得口罩产量在二月的基础上逐月提高,已知![]() 月份口罩产量为
月份口罩产量为![]() 万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水产养殖户开发一个三角形状的养殖区域,A、B、C三点的位置如图所示.已知∠CAB=105°,∠B=45°,AB=100![]() 米.(参考数据:
米.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)

(1)求养殖区域△ABC的面积;
(2)养殖户计划在边BC上选一点D,修建垂钓栈道AD,测得∠CAD=40°,求垂钓栈道AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
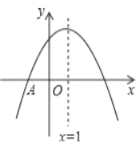
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ,
,![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() .其中结论正确的是( )
.其中结论正确的是( )
A.①B.②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以3元/本的价格购进某种笔记本若干,然后以5元/本的价格出售,每天售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若每本降价![]() 元,则每天的销售量是________本(用含
元,则每天的销售量是________本(用含![]() 的代数式表示).
的代数式表示).
(2)要想每天赢利60元,该超市需将每本的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.
(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____ cm.
(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
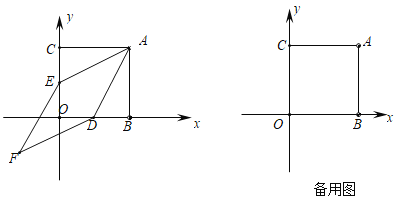
【题目】如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.
(1)求证:四边形AEFD为菱形.
(2)求四边形AEFD的面积.
(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com