练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，已知△ADE∽△ABC，且AD=3，BD=CE=4，求AC的长．
    考点：相似三角形的性质
    专题：
    分析：由相似可得到
    AD
    AB
    =
    AE
    AC
    ，结合条件求得AB代入可求得AC．
    解答：解：∵AD=3，BD=CE=4，
    ∴AB=AD+BD=3+4=7，AE=AC-EC=AC-4，
    ∵△ADE∽△ABC，
    ∴
    AD
    AB
    =
    AE
    AC
    ，
    ∴
    3
    7
    =
    AC-4
    AC
    ，
    解得AC=7．
    点评：本题主要考查相似三角形的性质，掌握相似三角形的对应边成比例是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    解方程：100（3x-1）+10x+（2x+1）-[100（2x+1）+10x+（3x-1）]=99．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，某船向正东航行，在A处望见海岛C在北偏东60°，前进6海里到B点，测得海岛C在北偏东45°，已知在该岛周围6海里内有暗礁，问船继续向正东航行，有触礁的危险吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若
    		(a-1)2
    =3，则a=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

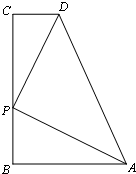    如图，已知四边形ABCD，∠B=∠C=90°，P是BC边上的一点，∠APD=90°．
    （1）求证：△ABP∽△PCD；
    （2）若BC=10，CD=3，PD=3
    		5
    ，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，D是BC的中点，且AD=AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．过C点作CG∥AD，交BA的延长线于G，过A作BC的平行线交CG于H点．
    （1）若∠BAC=90°，求证：四边形ADCH是菱形；
    （2）若DE=3，BC=8，求△FCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，在△ABC中，已知DE∥BC，CD平分∠ACB，∠B=70°，∠ACB=60°，求∠BDC和∠BDE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数与x轴交于（0，0），（12，0），且顶点到x轴的距离为3，求函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）（
    3
    5
    ）2=
     
    ；
    （2）（
    		3
    ）2=
     
    ；
    （3）（
    		0
    ）2=
     
    ；
    （4）
    		9
    =
     
    ；
    （5）
    		0.012
    =
     
    ；
    （6）
    		(-2)2
    =
     
    ．

    查看答案和解析>>

    同步练习册答案