
(本题满分12分)如图,抛物线 与x轴交于点A(1,0)和B(3,0).
与x轴交于点A(1,0)和B(3,0).

(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)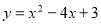 ;(2)C(4,3);(3)P(
;(2)C(4,3);(3)P(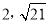 )或(
)或(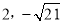 )或(
)或( )或(
)或(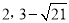 ).
).
【解析】
试题分析:(1)把点A、B的坐标代入函数解析式,解方程组求出a、b的值,即可得解;
(2)根据抛物线解析式求出对称轴,再根据平行四边形的对角线互相平分求出点C的横坐标,然后代入函数解析式计算求出纵坐标,即可得解;
(3)设AC、EF的交点为D,根据点C的坐标写出点D的坐标,然后分①O是顶角,②C是顶角,③P是顶角三种情况讨论.
试题解析:(1)把点A(1,0)和B(3,0)代入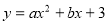 得,
得,
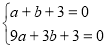 ,解得
,解得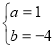 ,所以,抛物线的解析式为
,所以,抛物线的解析式为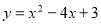 ;
;
(2)抛物线的对称轴为直线x=2,
∵四边形OECF是平行四边形∴点C的横坐标是4,
∵点C在抛物线上,∴ ,
,
∴点C的坐标为(4,3);
(3)∵点C的坐标为(4,3),∴OC的长为5,
①点O是顶角顶点时,OP=OC=5,
∵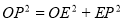 ,OE=2∴
,OE=2∴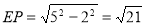 ,
,
所以,点P的坐标为(2,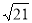 )或(2,-
)或(2,-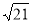 );
);
②点C是顶角顶点时,CP=OC=5,同理求出PF=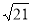 ,所以,PE=
,所以,PE=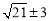 ,
,
所以,点P的坐标为(2,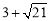 )或(2,
)或(2, 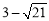 );
);
③点P是顶角顶点时,点P在OC上,不存在.
综上所述,抛物线的对称轴上存在点P(2,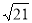 )或(2,-
)或(2,-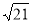 )或(2,
)或(2,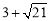 )或(2,
)或(2, 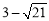 ),使△OCP是等腰三角形.
),使△OCP是等腰三角形.
考点:二次函数综合题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2014-2015学年湖北省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知二次函数当x=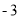 时,有最大值
时,有最大值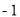 ,且当x=0时,y=
,且当x=0时,y= 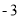 ,求二次函数的解析式。
,求二次函数的解析式。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c的图象如图,则a、b、c满足 ( )

A. a<0,b<0,c>0; B. a<0,b<0,c<0;
C. a<0,b>0,c>0; D. a>0,b<0,c>0。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市九年级上学期期中考试数学试卷(解析版) 题型:选择题
将抛物线 向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:填空题
(本题满分6分)如图,△ABC 的顶点A、B在⊙O上,边BC与⊙O 交于点D.①AB=AC;②BD=DC;③AB是⊙O的直径.此三个条件中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①② ③;①③
③;①③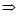 ②;②③
②;②③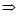 ①.
①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省八年级上学期第一次月考数学卷(解析版) 题型:填空题
一个多边形截去一个角后,形成的另一个多边形后的内角和为720°,那么原多边形的边数为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省通山县九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分9分)已知一元二次方程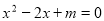 .
.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为 ,
, ,且
,且 ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列计算结果为-1的是( )
A. (-2)+(+3) B. (+1)-(-2) C. (-1)2014 D. (-3)÷(+3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com