
分析 (1)方程变形后,利用因式分解法求出解即可;
(2)方程变形后,利用因式分解法求出解即可;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(4)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)分解因式得:x(x-5)=0,
解得:x1=0,x2=5;
(2)分解因式得:(x-3)2=0,
开方得:x1=x2=3;
(3)去分母得:x2+x=x2-4,
解得:x=-4,
经检验x=-4是分式方程的解;
(4)去分母得:x-5=2x-5,
解得:x=0,
经检验x=0是分式方程的解.
点评 此题考查了解一元二次方程-因式分解法,配方法,以及解分式方程,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
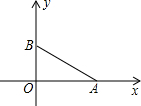 如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).
如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com