
【题目】如图,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_____.
的长为_____.
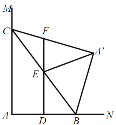
【答案】2或![]()
【解析】
![]() 与
与![]() 关于
关于![]() 所在直线对称,点D、E分别是AB、BC的中点,可得
所在直线对称,点D、E分别是AB、BC的中点,可得![]() =AC=2,∠B
=AC=2,∠B![]() C=∠A=90°,
C=∠A=90°,![]() B=AB,DE是△ABC的中位线,当
B=AB,DE是△ABC的中位线,当![]() 为直角三角形时,分情况讨论:①当∠
为直角三角形时,分情况讨论:①当∠![]() FE=90°时;②当∠
FE=90°时;②当∠![]() EF=90°时,分别画出图形计算即可得出答案.
EF=90°时,分别画出图形计算即可得出答案.
∵![]() 与
与![]() 关于
关于![]() 所在直线对称,点D、E分别是AB、BC的中点,
所在直线对称,点D、E分别是AB、BC的中点,
∴![]() =AC,∠B
=AC,∠B![]() C=∠A=90°,
C=∠A=90°,![]() B=AB,DE是△ABC的中位线,
B=AB,DE是△ABC的中位线,
当![]() 为直角三角形时,分情况讨论:
为直角三角形时,分情况讨论:
①当∠![]() FE=90°时,如图所示,DF∥AC,∠A=90°,
FE=90°时,如图所示,DF∥AC,∠A=90°,
∴DF⊥AB,DF⊥![]() C,
C,
∴![]() C∥AB,
C∥AB,
∴∠AC![]() =90°,即四边形AB
=90°,即四边形AB![]() C是矩形,
C是矩形,
又∵![]() B=AB,
B=AB,
∴矩形AB![]() C是正方形,
C是正方形,
∴AB=AC=2;
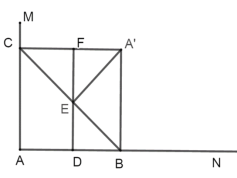
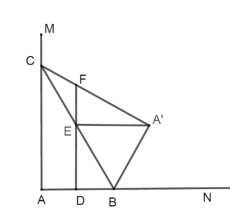
②当∠![]() EF=90°时,如图所示,
EF=90°时,如图所示,
∵![]() E∥AB,
E∥AB,![]() E=
E=![]() BC,
BC,
∴∠![]() EB=∠ABE=∠
EB=∠ABE=∠![]() BE,
BE,
∴![]() E=
E=![]() B=BE,
B=BE,
∴△![]() BE是等边三角形,∠
BE是等边三角形,∠![]() BE=60°,
BE=60°,
∵![]() C=AC=2,
C=AC=2,
∴![]() B=
B=![]() =
=![]() ,
,
∴AB=![]() ,
,
综上所述,AB的长度为2或![]() ,
,
故答案为:2或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为![]() .
.
(1)求反比例函数的表达式;
(2)设直线![]() 与
与![]()
![]() 轴,
轴,![]() 轴分别交于点C,D,且
轴分别交于点C,D,且![]() ,直接写出
,直接写出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
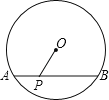
A.4个B.5个C.6个D.7个
查看答案和解析>>
科目:初中数学 来源: 题型:
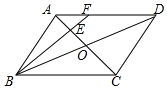
【题目】如图,在平行四边形ABCD中AC,BD相交于点O,点E是OA的中点,连接BE并延长AD于点F,已知△AEF的面积=1,则平行四边形ABCD的面积是( )
A.24B.18C.12D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书室计划购买了甲、乙两种故事书.若购买7本甲种故事书和4本乙种故事书需510元;购买3本甲种故事书和5本乙种故事书需350元.
(1)求甲种故事书和乙种故事书的单价;
(2)学校准备购买甲、乙两种故事书共200本,且甲种故事书的数量不少于乙种故事书的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
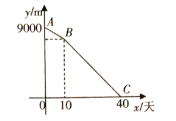
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
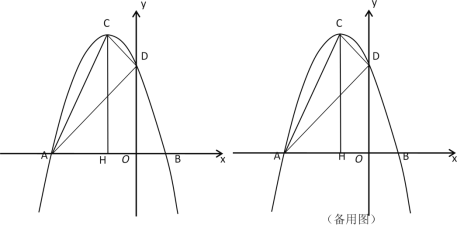
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com