练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
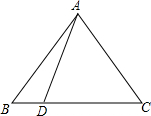
    如图，D为△ABC中BC边上一点，证明：AD2=AB2•
    DC
    BC
    +AC2•
    BD
    BC
    -BC2•
    BD
    BC
    •
    DC
    BC
    ．
    考点：勾股定理
    专题：证明题
    分析：过A点做BC垂线 交于E点，则BE=BD+DE，CE=DC-DE，根据勾股定理即可得出AB2•
    DC
    BC
    +AC2•
    BD
    BC
    -BC2•
    BD
    BC
    •
    DC
    BC
    =[AE2+（BD+DE）2]
    DC
    BC
    +[AE2+（DC-DE）2]
    BD
    BC
    -BD•DC，继而即可得出结论．
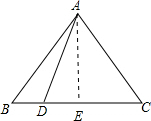    解答：解：过A点做BC垂线 交于E点，则BE=BD+DE，CE=DC-DE，
    ∵AB2•
    DC
    BC
    +AC2•
    BD
    BC
    -BC2•
    BD
    BC
    •
    DC
    BC

    =[AE2+（BD+DE）2]
    DC
    BC
    +[AE2+（DC-DE）2]
    BD
    BC
    -BD•DC
    =AD2•
    DC
    BC
    +
    BD
    BC
    （BD•DC）+
    2DE•BD•DC
    BC
    +AD2•
    BD
    BC
    +
    DC
    BC
    （BD•DC）-
    2DE•BD•DC
    BC
    -BD•DC
    =AD2•（
    BD
    BC
    +
    DC
    BC
    ）+（BD•DC）（
    BD
    BC
    +
    DC
    BC
    ）-BD•DC
    =AD2．
    ∴AD2=AB2•
    DC
    BC
    +AC2•
    BD
    BC
    -BC2•
    BD
    BC
    •
    DC
    BC
    ．
    点评：本题考查勾股定理的知识，解题关键是利用勾股定理将BE2、CE2化为（BD+DE）2和（DC-DE）2，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    根据下列表格中列出来的数值，可判断方程x2-bx-c=0有一个根大约是（　　）
    x00.511.52
    x2-bx-c-15-8.75-25.2513
    A、0.25B、0.75
    C、1.25D、1.75

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    1
    2
    x-2（x-
    1
    3
    y2）+（
    3
    2
    x+
    1
    3
    y2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （+26）+（-18）-（-5）+（-16）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知关于x的方程（m+1）x2+（m-3）x-（2m+1）=0，m取何值时，它是一元二次方程？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    对于任意实数x、y、z，定义运算“※”，满足x※y=
    6x2+4xy+y2-249
    (x+1)2+(y+1)2-57
    ，且x※y※z=（x※y）※z．在下列各结论中：①2※1=5；②x※3=6；③这一运算满足交换律，即x※y=y※x；④2014※2013※2012※…※4※3※2=19．其中正确的是
     
    （填编号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若单项式-3xmyn与3x2y3的和为0，则
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

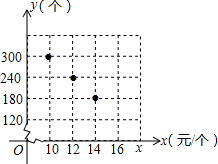    某商店准备购进一批茶杯进行销售，根据市场调查，这种茶杯一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示：
    （1）试判断y与x之间的函数关系，并求出函数关系式；
    （2）若茶杯的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；
    （3）若茶杯的进货成本不超过900元，要想获得最大的利润，试确定这种茶杯的销售单价，并求出此时的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知气温随高度升高而下降，下降的一般规律是从地面到高空11km高处，每升高1km，气温下降6℃；高于11km时，气温几乎不再变化，设某处地面气温20℃，该处高空xkm处气温为y℃．
    （1）当0≤x≤11时，求y关于x的函数关系式；
    （2）画出该处气温随高度（包括高于11km）而变化的图象；
    （3）试分别求出该处在离地面4.5km及13km的高空处的气温．

    查看答案和解析>>

    同步练习册答案