
 如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.分析 (1)先根据等边三角形的性质得∠OBA=∠CBD=60°,OB=BA,BC=BD,则∠OBC=∠ABD,然后可根据“SAS”可判断△OBC≌△ABD;
(2)由△OBC≌△ABD得到∠BAD=∠BOC=60°,则利用平角定义可计算出∠OAE=60° 然后在Rt△EOA中,利用正切定义可计算出OE=$\sqrt{3}$,从而得到点E的坐标为(0,$\sqrt{3}$),于是可判断点E的位置不发生变化;
(3)先计算出AE=2,再分类讨论:当EP=EA=2时,以点E为圆心,2为半径作圆交y轴的两个交点即为P点,容易得到此时P点坐标;当AE=AP时,此时点P与点E关于x轴对称,则P点坐标为(0,-$\sqrt{3}$);当PE=PA时,作AE的垂直平分线交y轴于P点,连结PA,如图,设P(0,t),则PE=PA=$\sqrt{3}$-t,在Rt△OPA中,利用勾股定理得到t2+12=($\sqrt{3}$-t)2,解得t=$\frac{3-\sqrt{3}}{6}$,此时P点坐标为(0,$\frac{3-\sqrt{3}}{6}$).
解答 解:(1)△OBC与△ABD全等.理由如下:
∵△AOB、△CBD都是等边三角形,
∴∠OBA=∠CBD=60°,OB=BA,BC=BD,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
$\left\{\begin{array}{l}{BO=BA}\\{∠OBC=∠ABD}\\{BC=BD}\end{array}\right.$,
∴△OBC≌△ABD;
(2)点E位置不变.
∵△OBC≌△ABD,
∴∠BAD=∠BOC=60°,
∴∠OAE=180°-60°-60°=60°
在Rt△EOA中,EO=OA•tan60°=$\sqrt{3}$,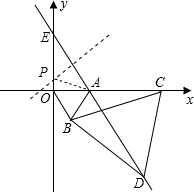
∴OE=$\sqrt{3}$,
∴点E的坐标为(0,$\sqrt{3}$);
(3)存在.
在Rt△EOA中,∵OE=1,OE=$\sqrt{3}$,
∴AE=2,
当EP=EA=2时,P点坐标为(0,2+$\sqrt{3}$)或(0,$\sqrt{3}$-2);
当AE=AP时,P点坐标为(0,-$\sqrt{3}$);
当PE=PA时,作AE的垂直平分线交y轴于P点,连结PA,如图,
设P(0,t),则PE=$\sqrt{3}$-t,
∴PA=$\sqrt{3}$-t,
在Rt△OPA中,t2+12=($\sqrt{3}$-t)2,解得t=$\frac{3-\sqrt{3}}{6}$,此时P点坐标为(0,$\frac{3-\sqrt{3}}{6}$).
综上所述,满足条件的P点坐标为(0,2+$\sqrt{3}$)或(0,$\sqrt{3}$-2)或(0,$\frac{3-\sqrt{3}}{6}$).
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.也考查了等边三角形的判定与性质.解决本题的关键是利用分类讨论的思想求P点坐标.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:解答题
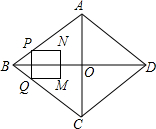 如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
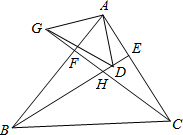 如图,在△ABC中,BE,CF分别是AC,AB边上的高,在BE上截取BD=AC,延长CF至G,使CG=AB,连接AD,AG,GD,试判断△AGD的形状.
如图,在△ABC中,BE,CF分别是AC,AB边上的高,在BE上截取BD=AC,延长CF至G,使CG=AB,连接AD,AG,GD,试判断△AGD的形状.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com