
����Ŀ����ѧ�
(1)�龳�۲�
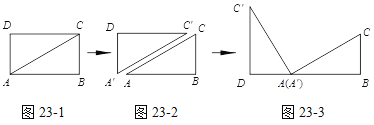
������ֽƬABCD�ضԽ���AC�������õ���ABC�͡�A��C��D����ͼ23-1��ʾ.����A��C��D�Ķ���A�����A�غϣ����Ƶ�A(A��)����ʱ�뷽����ת��ʹ��D��A(A��)��B��ͬһ��ֱ���ϣ���ͼ23-2��ʾ��
�۲�ͼ23-2��֪����BC��ȵ��߶��� ����CAC��= �ȣ�
(2)����̽��
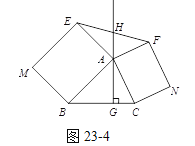
��ͼ23-3����ABC�У�AG��BC�ڵ�G����AΪֱ�Ƕ��㣬�ֱ���AB��ACΪֱ�DZߣ����ABC��������Rt��ABE�͵���Rt��ACF������E��F������GA�Ĵ��ߣ�����ֱ�ΪP��Q. ��̽��EP��FQ֮���������ϵ����֤����Ľ���.
(3)��չ����
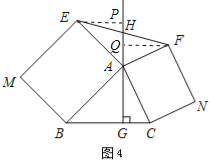
��ͼ23-4����ABC�У�AG��BC�ڵ�G���ֱ���AB��ACΪһ�����ABC��������ABME�;���ACNF������GA��EF�ڵ�H. ��AB=k��AE��AC=k��AF����̽��HE��HF֮���������ϵ����˵������.
���𰸡���1��DA��90����2��FQ=EP��֤�����£���3��HE=HF����������.
���������⣺��1����ͼ2������ת�����ʿ�֪����ABC�ա�A��C��D��
��BC=A��D����ACB=��C��AD������ACB+��CAB=90����
���C��AD+��CAB=90��������CAC��=90����
�ʴ�Ϊ��A��D��=90����
��2��EP=FQ��
֤�����ߡ�ABE�ǵ���ֱ�������Σ�
���EAB=90��������EAP+��BAG=90��������ABG+��BAG=90����
���EAP=��ABG��
����APE����BGA��
![]() ��
��
���APE�ա�BGA��
��EP=AG��
ͬ����FQ=AG��
��EP=FQ��
��3��HE=HF��
֤������EP��GA��GA���ӳ�����P����FQ��GA��GA���ӳ�����Q��
���ı���ABME�Ǿ��Σ�
���EAB=90��������EAP+��BAG=90��������ABG+��BAG=90����
���EAP=��ABG������APE=��BGA=90����
���APE�ס�BGA��
��![]() =����AG=kEP��
=����AG=kEP��
ͬ����AQF�ס�CGA��
��![]() =k����AG=kFQ��
=k����AG=kFQ��
��EP=FQ��
��EP��GA��FQ��GA��
��EP��FQ����EP=FQ��
��HE=HF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B��C���ǡ�ABCƽ�ƺ�õ��ģ�����ABC�������������ֱ�ΪA(��2��3)��B(��4����1)��C(2��0)������ƽ�ƺ�A��������Ϊ(3��6)������Ӧ��B�䣬C�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��yΪ�κ�ʵ����x2+y2��4x��2y+8��ֵ���ǣ� ��
A.����
B.����
C.�Ǹ���
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
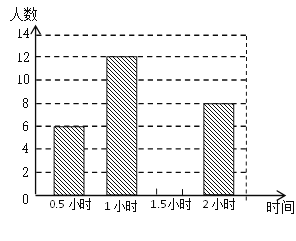
����Ŀ��Ϊ�˹᳹��������Ч���������վ��꼶600��ѧ��ÿ�������ѧϰ�����ijУ�������˾��꼶�IJ���ѧ��������������ÿ������ѧϰ��ʱ�䣮���ݵ�������������������������ͳ��ͼ���£������ͳ��ͼ�е���Ϣ�ش��������⣺
��1���˴γ��������У��������˶�����ѧ����
��2����ͼ21-1����������
��3�����ͼ21-2��Բ�Ľ�![]() �Ķ�����
�Ķ�����
��4��������У���꼶ѧ������ѧϰʱ�䲻����1.5Сʱ���ж����ˣ�
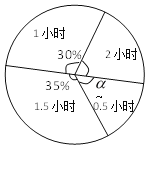
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��S1=1+ ![]() +
+ ![]() ��S2=1+
��S2=1+ ![]() +
+ ![]() ��S3=1+
��S3=1+ ![]() +
+ ![]() ��S4=1+
��S4=1+ ![]() +
+ ![]() ��S5=1+
��S5=1+ ![]() +
+ ![]() ������
������ ![]() =���ú�n�Ĵ���ʽ��ʾ������nΪ��������
=���ú�n�Ĵ���ʽ��ʾ������nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(m��3��2)���B(1��n��1)����x��Գƣ���m��________��n��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��C=30�㣬AC=48����D�ӵ�C������CA������ÿ��4����λ�����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������ÿ��2����λ�����ٶ����B�����˶���������һ���㵽���յ㣬��һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��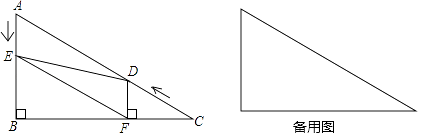
��1����֤��AE=DF��
��2�����ı���BFDE�Ǿ���ʱ����t��ֵ��
��3���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com