
分析 设直线y=kx+b,经过A(0,2)和B(3,0)两点,代入可求出函数关系式.
解答 解:设直线为y=kx+b,
∵经过A(0,2)和B(3,0)两点,
∴$\left\{\begin{array}{l}{b=2}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=2}\end{array}\right.$,
∴这个一次函数关系式是y=-$\frac{2}{3}$x+2.
故答案为y=-$\frac{2}{3}$x+2.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
| 人数 | 不超过30人 | 超过30人但不超过40人 | 超过40人 |
| 人均旅游费 | 1000元 | 每增加1人,人均旅游费降低20元 | 800元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
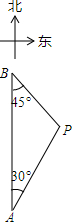 如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
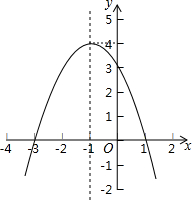 已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:
已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com