
【题目】如图,某公安海上缉私局发现在我国领海的P处有一条走私船正以22海里/时的速度沿南偏东64的方向向公海逃窜,于是缉私局命令位于点P北偏东30方向A处的我公安缉私快艇前往拦截,已知P、A相距20海里,公安缉私快艇向正南方向行进计划在B处拦截走私船。
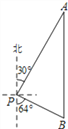
(1)求A、B两处的距离;(结果保留整数)
(2)若公安缉私快艇要在B处成功拦截走私船,则缉私快艇的速度至少为多少海里/时?
【参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2,![]() ,
,![]() ,
,![]() 】
】
【答案】(1) 22 海里;(2) 至少为44海里/小时.
【解析】分析:(1)过P点作PC⊥AB于点C,首先在RT△APC中,求得AC的长,然后在直角△BCP中,求得BC的长,再根据AB=AC+BC计算即可;(2)首先求得PB的距离,根据走私船的速度,求出时间,然后再根据AB=22, 设缉私快艇的速度为v,可求出缉私快艇的时间,两者比较,从而求解.
详解:(1)过P点作PC⊥AB于点C
Rt△APC中,∵ ∠A=30°,PA=20
∴ AC=![]() ,PC=10,
,PC=10,
Rt△PBC中,∵∠B=64°
∴ tan64°=![]() =2 PC=5
=2 PC=5
∴ AB=![]() +5 ≈22 海里 .
+5 ≈22 海里 .
(2)Rt△PBC中,∵BC=5,PC=10
∴PB=![]()
设走私船到B点时间为t,则t=![]()
设公安缉私船速度为V,则由题意 ![]() 解得 V≥44
解得 V≥44
答:缉私船的速度至少为44海里/小时才能在B拦截走私船。


科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
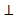
(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将![]() 、
、![]() 称为一对“对偶式”,因为
称为一对“对偶式”,因为![]()
![]() ,所以构造“对偶式”再将其相乘可以有效的将
,所以构造“对偶式”再将其相乘可以有效的将![]() 和
和![]() 中的“
中的“![]() ”去掉.于是二次根式除法可以这样解:如
”去掉.于是二次根式除法可以这样解:如![]() ,
,![]()
![]() .像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
.像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)比较大小![]() ________
________![]() (用“
(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空);
”填空);
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法.
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线.
(2)如图2,在8×6的正方形网格中,请用无刻度直尺画一个与△ABC面积相等,且以BC为边的平行四边形,顶点在格点上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]() ;
;
按规律填空
(1)![]() +
+![]() +
+![]() +
+![]() =______;
=______;
(2)![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() =________;
=________;
(3)如果n为正整数,那么
![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() =______;
=______;
(4)由此拓展写出具体过程:
![]() +
+![]() +
+![]() +…+
+…+![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
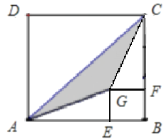
【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
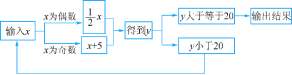
【题目】按如图所示的程序计算,若输入的值x=17,则输出的结果为22;若输入的值x=34,则输出的结果为22.当输出的值为24时,则输入的x的值在0至40之间的所有正整数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
①(-8)+6-(-13)+(-6);
②![]()
③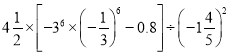
④5(3a2b-ab2+c)-4(2c-ab2+3a2b)
⑤3x2 -[7x - 2(4x + 2) +2x2]-x2
⑥-14-![]() ÷3×[3-(-3)2].
÷3×[3-(-3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com