科目：初中数学 来源： 题型：
如图，在△ABC中，AB=AC，∠B=60°，
∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，
CD平分∠
ECA．
(1) 求证：四边形ABCD是菱形．
(2) 若AB=2,连接BD，求BD长。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：(1)AE=BF；(2)AE⊥BF；(3)AO=OE；(4)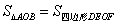
中正确的有( )
A．4个 B．3个 C．2个 D．1个
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
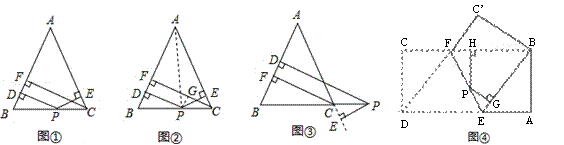
【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥
AB，垂足为F．求证：PD+PE=CF．小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF． 小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
(1) 从小军
和小俊的思路中任选一种方法，证明PD+PE=CF。
【变式探究】
(2) 如图3，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE=CF；
【结论运用】请运用上述解答中所积累的经验和方法完成下列题目：
(3) 如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=16，CF=6，求PG+PH的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，平行四边形 ABCD对角线交于点O，点E是线段BO上的动点（与点B、O不重合），连接CE，过A点作AF∥CE交BD于点F，连接AE与CF．
（1）求证：四边形AECF是平行四边形；
（2）当BA=BC=2，∠ABC=60°时，平行四边形 AECF能否成为正方形？若能，求出BE的长；若不能，请说明理由．
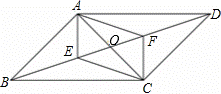
第23题
查看答案和解析>>
科目：初中数学 来源： 题型：
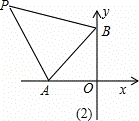
如图，A、B两点同时从原点O出发，点A以每秒x个单位长度沿x轴的负方向运动，点B以每秒y个单位长度沿y轴的正方向运动．
（1）若|x+2y﹣5|+|2x﹣y|=0，试分别求出1秒钟后A、B两点的坐标；
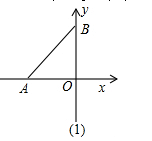
（2）设∠BAO的外角和∠ABO的外的平分线相交于点P，
问：点A、B在运动的过程中，∠P的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
有意义，则a的取值范围是______________
=
+
与正比例函数y =
（
、
≠0）的图象的是【 】
与直线
在同一平面直角坐标系中的图象如图所示，则关于
的不等式
的解集为 ．