
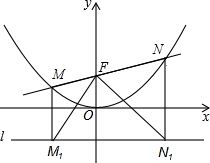
 ��ͼ������F��0��1����ֱ��y=kx+b��������y=$\frac{1}{4}$x2����M��x1��y1����N��x2��y2�����㣨����x1��0��x2��0����
��ͼ������F��0��1����ֱ��y=kx+b��������y=$\frac{1}{4}$x2����M��x1��y1����N��x2��y2�����㣨����x1��0��x2��0�������� ��1������ֱ��y=kx+b������F��0��1�����ɵõ�b��ֵ��
��2�����������̣����x��ֵ���������y��ֵ�����������M�͵�N�����ꣻ
��3����ֱ��y=kx+b��������y=$\frac{1}{4}$x2����M��x1��y1����N��x2��y2�����㣬�ֱ���x1��x2��ʾ��NF2��NN12��FM12��FN12��M1N12���ݴ˿��������жϣ�
��� �⣺��1����ֱ��y=kx+b������F��0��1����
��b=1��
��2����k=1ʱ��ֱ��y=x+1��
���������֪��$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$��
��$\frac{1}{4}$x2=x+1��
���x1=-2$\sqrt{2}$+2��x2=2$\sqrt{2}$+2��
��x=-2$\sqrt{2}$+2ʱ��y=-2$\sqrt{2}$+3������M����Ϊ��-2$\sqrt{2}$+2��-2$\sqrt{2}$+3����
��x=2$\sqrt{2}$+2ʱ��y=2$\sqrt{2}$+3������N������Ϊ��2$\sqrt{2}$+2��2$\sqrt{2}$+3����
��3����k=1ʱ����NFN1�ǵ��������Σ���M1FN1��ֱ�������Σ�
��ֱ��y=kx+b��������y=$\frac{1}{4}$x2����M��x1��y1����N��x2��y2�����㣬
����Եó���kx+b=$\frac{1}{4}$x2��
�����ã�$\frac{1}{4}$x2-kx-1=0��
��a=$\frac{1}{4}$��c=-1��
��x1•x2=-4��
��NFN1�ǵ��������Σ�
�����ǣ�NF2=x22+��y2-1��2=x22+y22-2y2+1=y22+$\frac{1}{2}$x22+1��
NN12=��y2+1��2=y22+2y2+1=y22+$\frac{1}{2}$x22+1��
��NF2=NN12��
����NFN1�ǵ��������Σ�
��M1FN1��ֱ�������Σ�F����ֱ�Ƕ��㣩��
�������£���ֱ��l��y��Ľ�����F1��
FM12=FF12+M1F12=x12+4��
FN12=FF12+F1N12=x22+4��
M1N12=��x1-x2��2=x12+x22-2x1x2=x12+x22+8��
��FM12+FN12=M1N12��
���M1FN1����F��Ϊֱ�Ƕ����ֱ�������Σ�
���� ������Ҫ�����˶��κ����ۺ��⣬�õ���֪ʶ����һԪ���η��̸���ϵ���Ĺ�ϵ�����������ε��ж���ֱ�������ε��ж��Լ����ɶ�����֪ʶ�����3���ʹؼ��Ƿֱ�����x1��x2��ʾ��NF2��NN12��FM12��FN12��M1N12����Ŀ���ۺ��Բ�С����ѧ������������Ҫ��Ҳ�ܸߣ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
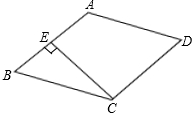 ��ͼ��������ABCD�У�CE��AB�ڵ�E����֪��BCE=30�㣬CE=3cm��������ABCD���ܳ��������
��ͼ��������ABCD�У�CE��AB�ڵ�E����֪��BCE=30�㣬CE=3cm��������ABCD���ܳ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
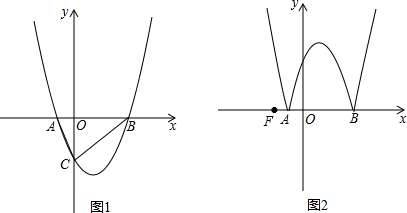
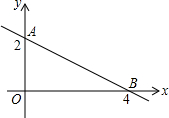 ��ͼ��ֱ��AB��y�ᣬx��Ľ���ΪA��B���㣬��A��B�������ꡢ��������ͼ��ʾ����x�����Ƿ����һ��p��ʹS��PAB=3�������ڣ����P������꣬�������ڣ�˵�����ɣ�
��ͼ��ֱ��AB��y�ᣬx��Ľ���ΪA��B���㣬��A��B�������ꡢ��������ͼ��ʾ����x�����Ƿ����һ��p��ʹS��PAB=3�������ڣ����P������꣬�������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com