
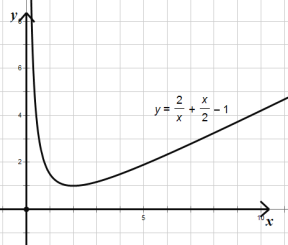
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐy=y1+y2Θ§Τδ÷–y1”κx≥…Ζ¥±»άΐΘ§y2”κx©¹2≥…’ΐ±»άΐΘ§Κ· ΐΒΡΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß «x![]() Θ§«“Β±x=1Μρx=4 ±Θ§yΒΡ÷ΒΨυΈΣ
Θ§«“Β±x=1Μρx=4 ±Θ§yΒΡ÷ΒΨυΈΣ![]() Θ°
Θ°
«κΕ‘ΗΟΚ· ΐΦΑΤδΆΦœσΫχ––»γœ¬ΧΫΨΩΘΚ
Θ®1Θ©ΫβΈω ΫΧΫΨΩΘΚΗυΨίΗχΕ®ΒΡΧθΦΰΘ§Ω…“‘»ΖΕ®≥ωΗΟΚ· ΐΒΡΫβΈω ΫΈΣΘΚΓΓ ΓΓΘ°
Θ®2Θ©Κ· ΐΆΦœσΧΫΨΩΘΚ
ΔΌΗυΨίΫβΈω ΫΘ§≤Ι»Ϊœ¬±μΘΚ
ΔΎΗυΨί±μ÷– ΐΨίΘ§‘Ύ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψΘ§≤ΔΜ≠≥ωΚ· ΐΆΦœσ
Θ®3Θ©ΫαΚœΜ≠≥ωΒΡΚ· ΐΆΦœσΘ§ΫβΨωΈ ΧβΘΚ
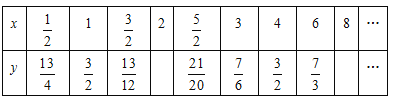
ΔΌΒ±x![]() Θ§
Θ§![]() Θ§8 ±Θ§Κ· ΐ÷ΒΖ÷±πΈΣy1Θ§y2Θ§y3Θ§‘ρy1Θ§y2Θ§y3ΒΡ¥σ–ΓΙΊœΒΈΣΘΚΓΓ ΓΓΘΜΘ®”ΟΓΑΘΦΓ±ΜρΓΑ=Γ±±μ ΨΘ©
Θ§8 ±Θ§Κ· ΐ÷ΒΖ÷±πΈΣy1Θ§y2Θ§y3Θ§‘ρy1Θ§y2Θ§y3ΒΡ¥σ–ΓΙΊœΒΈΣΘΚΓΓ ΓΓΘΜΘ®”ΟΓΑΘΦΓ±ΜρΓΑ=Γ±±μ ΨΘ©
ΔΎ»τ÷±œΏy=k”κΗΟΚ· ΐΆΦœσ”–ΝΫΗωΫΜΒψΘ§‘ρkΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ§¥Υ ±Θ§xΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΔΌ¥πΑΗΦϊΫβΈωΘΜΔΎ¥πΑΗΦϊΫβΈωΘΜΘ®3Θ©ΔΌy2ΘΦy1ΘΦy3ΘΜΔΎ1ΘΦk
ΘΜΘ®2Θ©ΔΌ¥πΑΗΦϊΫβΈωΘΜΔΎ¥πΑΗΦϊΫβΈωΘΜΘ®3Θ©ΔΌy2ΘΦy1ΘΦy3ΘΜΔΎ1ΘΦk![]() Θ§
Θ§![]() xΘΦ2Μρ2ΘΦxΓή8Θ°
xΘΦ2Μρ2ΘΦxΓή8Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”Ο¥ΐΕ®œΒ ΐΖ®…η![]() Θ§y2=k2Θ®x-2Θ©Θ§‘ρ
Θ§y2=k2Θ®x-2Θ©Θ§‘ρ![]() +k2(x2)Θ§ΫΪ“―÷ΣΧθΦΰ¥ζ»κΒΟΙΊ”Ύk1ΓΔk2ΖΫ≥ΧΉιΘ§Φ¥Ω…«σΒΟΗΟΚ· ΐΫβΈω ΫΘΜ
+k2(x2)Θ§ΫΪ“―÷ΣΧθΦΰ¥ζ»κΒΟΙΊ”Ύk1ΓΔk2ΖΫ≥ΧΉιΘ§Φ¥Ω…«σΒΟΗΟΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©―ûà ± ΐ÷ΒΧν±μΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψΘ§”ΟΤΫΜ§«ζœΏ¥”ΉσΒΫ”“Υ≥¥ΈΝ§Ϋ”ΗςΒψΘ§Μ≠≥ωΆΦœσΘΜ
Θ®3Θ©Ιέ≤λΆΦœσΘ§ΒΟ≥ωΫα¬έΘ°
Θ®1Θ©…η![]() Θ§y2=k2Θ®x©¹2Θ©Θ§‘ρ
Θ§y2=k2Θ®x©¹2Θ©Θ§‘ρ![]() Θ§
Θ§
”…Χβ“βΒΟΘΚ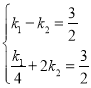 Θ§
Θ§
ΫβΒΟΘΚ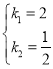 Θ§
Θ§
ΓύΗΟΚ· ΐΫβΈω ΫΈΣ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() Θ§
Θ§
Θ®2Θ©ΔΌΗυΨίΫβΈω ΫΘ§
Β±x=2 ±Θ§![]() ΘΜ
ΘΜ
Β±x=8 ±Θ§![]() ΘΜ
ΘΜ
≤Ι»Ϊœ¬±μΘΚ

ΔΎΗυΨί…œ±μ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψΘ§Μ≠≥ωΆΦœσΘ°
Θ®3Θ©ΔΌ”…Θ®2Θ©÷–ΆΦœσΩ…ΒΟΘΚΘ®2Θ§1Θ© «ΆΦœσ…œΉνΒΆΒψΘ§‘ΎΗΟΒψΉσ≤ύΘ§yΥφx‘ω¥σΕχΦθ–ΓΘΜ‘ΎΗΟΒψ”“≤ύyΥφx‘ω¥σΕχ‘ω¥σΘ§
ΓΏΒ±x![]() Θ§
Θ§![]() Θ§8 ±Θ§Ε‘”ΠΒΡΚ· ΐ÷ΒΖ÷±πΈΣy1Θ§y2Θ§y3Θ§
Θ§8 ±Θ§Ε‘”ΠΒΡΚ· ΐ÷ΒΖ÷±πΈΣy1Θ§y2Θ§y3Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Γύy2ΘΦy1ΘΦy3Θ° Ι ¥πΑΗΈΣΘΚy2ΘΦy1ΘΦy3Θ° ΔΎΙέ≤λΆΦœσΒΟΘΚx ΓύΒ±÷±œΏy=k”κΗΟΆΦœσ”–ΝΫΗωΫΜΒψ ±Θ§1ΘΦk ¥Υ ±xΒΡΖΕΈß «ΘΚ Ι ¥πΑΗΈΣΘΚ1ΘΦk![]() Θ§ΆΦœσΉνΒΆΒψΈΣΘ®2Θ§1Θ©Θ§
Θ§ΆΦœσΉνΒΆΒψΈΣΘ®2Θ§1Θ©Θ§![]() Θ§
Θ§![]() xΘΦ2Μρ2ΘΦxΓή8Θ°
xΘΦ2Μρ2ΘΦxΓή8Θ°![]() Θ§
Θ§![]() xΘΦ2Μρ2ΘΦxΓή8Θ°
xΘΦ2Μρ2ΘΦxΓή8Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
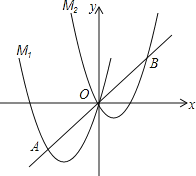
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪ≈ΉΈοœΏM1ΘΚyΘΫax2+4xœρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρ…œΤΫ“Τ3ΗωΒΞΈΜΘ§ΒΟΒΫ≈ΉΈοœΏM2Θ§÷±œΏyΘΫx”κM1ΒΡ“ΜΗωΫΜΒψΦ«ΈΣAΘ§”κM2ΒΡ“ΜΗωΫΜΒψΦ«ΈΣBΘ§ΒψAΒΡΚαΉχ±ξ «©¹3Θ°
Θ®1Θ©«σaΒΡ÷ΒΦΑM2ΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΒψC «œΏΕΈAB…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψCΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣDΘ§‘ΎCDΒΡ”“≤ύΉς’ΐΖΫ–ΈCDEFΘ°
ΔΌΒ±ΒψCΒΡΚαΉχ±ξΈΣ2 ±Θ§÷±œΏyΘΫx+n«ΓΚΟΨ≠Ιΐ’ΐΖΫ–ΈCDEFΒΡΕΞΒψFΘ§«σ¥Υ ±nΒΡ÷ΒΘΜ
ΔΎ‘ΎΒψCΒΡ‘ΥΕ·Ιΐ≥Χ÷–Θ§»τ÷±œΏyΘΫx+n”κ’ΐΖΫ–ΈCDEF Φ÷’ΟΜ”–ΙΪΙ≤ΒψΘ§«σnΒΡ»Γ÷ΒΖΕΈßΘ®÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§BCΘΫ4Θ§Γ―P”κΓςABCΒΡ±ΏΜρ±ΏΒΡ―”≥ΛœΏœύ«–Θ°»τΓ―PΑκΨΕΈΣ2Θ§ΓςABCΒΡΟφΜΐΈΣ5Θ§‘ρΓςABCΒΡ÷ή≥ΛΈΣ( )
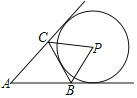
A.8B.10C.13D.14
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,ΗέΩΎA‘ΎΙέ≤β’ΨOΒΡ’ΐΕΪΖΫœρ,OA=4.Ρ≥¥§¥”ΗέΩΎA≥ωΖΔ,―Ί±±ΤΪΕΪ15ΓψΖΫœρΚΫ––“ΜΕΈΨύάκΚσΒΫ¥οB¥Π,¥Υ ±¥”Ιέ≤β’ΨO¥Π≤βΒΟΗΟ¥§ΈΜ”Ύ±±ΤΪΕΪ60ΓψΒΡΖΫœρ,‘ρΗΟ¥§ΚΫ––ΒΡΨύάκ(Φ¥ABΒΡ≥Λ)ΈΣ____.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊΙΊ”ΎxΒΡ≤ΜΒ» ΫΉι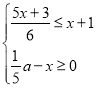 ÷Ν…Ό”–3Ηω’ϊ ΐΫβΘ§«“ΙΊ”ΎxΒΡΖ÷ ΫΖΫ≥Χ
÷Ν…Ό”–3Ηω’ϊ ΐΫβΘ§«“ΙΊ”ΎxΒΡΖ÷ ΫΖΫ≥Χ![]() ΒΡΫβΈΣ’ϊ ΐΘ§‘ρΖϊΚœΧθΦΰΒΡΥυ”–’ϊ ΐaΒΡ»Γ÷Β÷°ΚΆΈΣΘ®ΓΓΓΓΘ©
ΒΡΫβΈΣ’ϊ ΐΘ§‘ρΖϊΚœΧθΦΰΒΡΥυ”–’ϊ ΐaΒΡ»Γ÷Β÷°ΚΆΈΣΘ®ΓΓΓΓΘ©
A.©¹10B.©¹9C.©¹7D.©¹3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
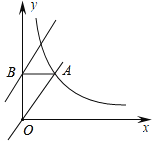
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐ±»άΐΚ· ΐyΘΫkx”κΖ¥±»άΐΚ· ΐyΘΫ![]() ΒΡΆΦœσ”–“ΜΗωΫΜΒψAΘ®mΘ§4Θ©Θ§ABΓΆy÷α”ΎΒψBΘ§ΤΫ“Τ÷±œΏyΘΫkxΘ§ ΙΤδΨ≠ΙΐΒψBΘ§ΒΟΒΫ÷±œΏlΘ§‘ρ÷±œΏlΕ‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «_____Θ°
ΒΡΆΦœσ”–“ΜΗωΫΜΒψAΘ®mΘ§4Θ©Θ§ABΓΆy÷α”ΎΒψBΘ§ΤΫ“Τ÷±œΏyΘΫkxΘ§ ΙΤδΨ≠ΙΐΒψBΘ§ΒΟΒΫ÷±œΏlΘ§‘ρ÷±œΏlΕ‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
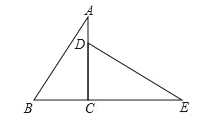
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§ΓςDCE «ΓςABC»ΤΉ≈ΒψCΥ≥ ±’κΖΫœρ–ΐΉΣΒΟΒΫΒΡΘ§¥Υ ±BΓΔCΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ°
Θ®1Θ©–ΐΉΣΫ«ΒΡ¥σ–ΓΘΜ
Θ®2Θ©»τAB=10Θ§AC=8Θ§«σBEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΦΚ÷Σ![]() Θ§
Θ§![]() Θ°Βψ
Θ°Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·ΘΜΒψ
ΒΡΥΌΕ»“ΤΕ·ΘΜΒψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±ΏΡΎΒψ
±ΏΡΎΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ°»γΙϊ
ΒΡΥΌΕ»“ΤΕ·Θ°»γΙϊ![]() ΓΔ
ΓΔ![]() Ά§ ±≥ωΖΔΘ§”Ο
Ά§ ±≥ωΖΔΘ§”Ο![]() ±μ Ψ“ΤΕ·ΒΡ ±Φδ
±μ Ψ“ΤΕ·ΒΡ ±Φδ![]() Θ°
Θ°
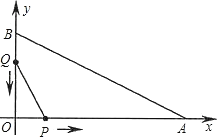
Θ®1Θ©”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘΚœΏΕΈ
ΒΡ¥ζ ΐ Ϋ±μ ΨΘΚœΏΕΈ![]() _______
_______![]() ΘΜ
ΘΜ![]() ______
______![]() ΘΜ
ΘΜ
Θ®2Θ©Β±![]() ΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–Έ
ΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ°
Θ°
Θ®3Θ©Β±![]() ”κ
”κ![]() œύΥΤ ±Θ§«σ≥ω
œύΥΤ ±Θ§«σ≥ω![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
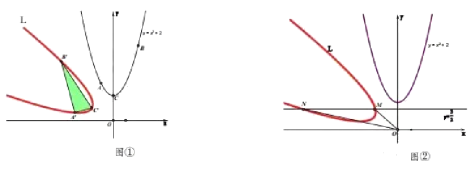
ΓΨΧβΡΩΓΩΕ®“εΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Έ“Ο«ΫΪΚ· ΐ![]() ΒΡΆΦœσ»Τ‘≠Βψ
ΒΡΆΦœσ»Τ‘≠Βψ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΚσΒΟΒΫΒΡ–¬«ζœΏ
ΚσΒΟΒΫΒΡ–¬«ζœΏ![]() ≥ΤΈΣΓΑΡφ–ΐ≈ΉΈοœΏΓ±.
≥ΤΈΣΓΑΡφ–ΐ≈ΉΈοœΏΓ±.
Θ®1Θ©»γΆΦΔΌΘ§ΦΚ÷ΣΒψ![]() Θ§
Θ§![]() ‘ΎΚ· ΐ
‘ΎΚ· ΐ![]() ΒΡΆΦœσ…œΘ§≈ΉΈοœΏΒΡΕΞΒψΈΣ
ΒΡΆΦœσ…œΘ§≈ΉΈοœΏΒΡΕΞΒψΈΣ![]() Θ§»τ
Θ§»τ![]() …œ»ΐΒψ
…œ»ΐΒψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() «
«![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() –ΐΉΣΚσΒΡΕ‘”ΠΒψΘ§Ν§Ϋα
–ΐΉΣΚσΒΡΕ‘”ΠΒψΘ§Ν§Ϋα![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() Θ§‘ρ
Θ§‘ρ![]() __________ΘΜ
__________ΘΜ
Θ®2Θ©»γΆΦΔΎΘ§Ρφ–ΐ≈ΉΈοœΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§‘ρ
Θ§‘ρ![]() __________Θ°
__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com