
【题目】某飞机着陆后滑行的距离y(米)关于着陆后滑行的时间x(秒)的函数关系是y=﹣2x2+bx(b为常数).若该飞机着陆后滑行20秒才停下来,则该型飞机着陆后的滑行距离是_____米.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
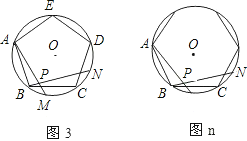
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
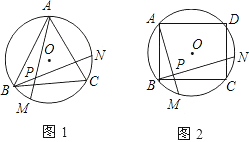
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有![]() 张床位的旅馆,当每张床位每天收费
张床位的旅馆,当每张床位每天收费![]() 元时,床位可全部租出.若每张床位每天收费提高
元时,床位可全部租出.若每张床位每天收费提高![]() 元,则相应的减少了
元,则相应的减少了![]() 张床位租出.如果每张床位每天以
张床位租出.如果每张床位每天以![]() 元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
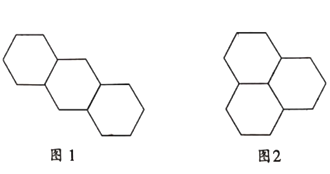
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
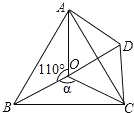
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-(2k-1)x+k2,其中k是常数.
(1)若该抛物线与x轴有交点,求k的取值范围;
(2)若此抛物线与x轴其中一个交点的坐标为(-1,0),试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;②做n次随机试验,事件A发生m次,则事件A发生的概率一定等于![]() ;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
(1)求直线![]() 的表达式;
的表达式;
(2)过点A做平行于x轴的直线l,l与抛物线![]() (a>0)交于B,C两点。若BC≥4,求a的取值范围;
(a>0)交于B,C两点。若BC≥4,求a的取值范围;
(3)设直线![]() 与抛物线
与抛物线![]() 交于D,E两点,当3
交于D,E两点,当3![]() ≤DE≤5
≤DE≤5![]() 时,结合函数的图象,直接写出m的取值范围是____________________。
时,结合函数的图象,直接写出m的取值范围是____________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
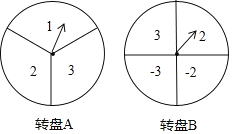
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com