
【题目】为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 | 优秀 | 良好 | 合格 | 不合格 |
人数 | m | 30 | n | 5 |
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好以上的学生有多少人?
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)

科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,点A,B分别在坐标轴上.
(1)如图①,若点C的横坐标为5,求点B的坐标.
(2)如图②,若BC交x轴于M,过C作CD⊥BC交y轴于D . 求证:BC-CD=MC.
(3)如图③,若点A的坐标为(-4,0),点B是y轴正半轴上的一个动点,分别以OB,AB为直角边在第一、第二象限作等腰Rt△OBF(∠OBF=90°)、等腰Rt△ABE(∠ABE=90°),连接EF交y轴于点P,当点B在y轴上运动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
我区在一项工程招标时,接到甲、乙两个工程队的投标书,从投标书中得知:每施工一天,甲工程队要![]() 万元,乙工程队要
万元,乙工程队要![]() 万元,工程小组根据甲、乙两队标书的测算,有三种方案:
万元,工程小组根据甲、乙两队标书的测算,有三种方案:![]() 甲队单独完成这个工程,刚好如期完成;
甲队单独完成这个工程,刚好如期完成;![]() 乙队单独完成这个工程要比规定时间多用5天;
乙队单独完成这个工程要比规定时间多用5天;![]() **********,剩下的工程由乙队单独做,也正好如期完成. 方案
**********,剩下的工程由乙队单独做,也正好如期完成. 方案![]() 中“星号”部分被损毁了. 已知,一个同学设规定的工期为
中“星号”部分被损毁了. 已知,一个同学设规定的工期为![]() 天,根据题意列出方程:
天,根据题意列出方程:![]()
(1)请将方案中“星号”部分补充出来________________;
(2)你认为哪个方案节省工程款,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为 2000 元,1700 元的A,B两种型号的净水器,下表是近两周的销售情况:
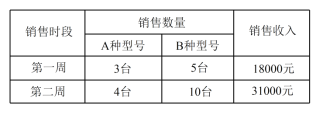
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台,求 A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() (3m+1)x﹣m(m>
(3m+1)x﹣m(m>![]() 且为实数)与x轴分别交于点A、B(点B位于点A的右侧且AB≠OA),与y轴交于点C.
且为实数)与x轴分别交于点A、B(点B位于点A的右侧且AB≠OA),与y轴交于点C.

(1)填空:点B的坐标为 ,点C的坐标为 (用含m的代数式表示);
(2)当m=3时,在直线BC上方的抛物线上有一点M,过M作x轴的垂线交直线BC于点N,求线段MN的最大值;
(3)在第四象限内是否存在点P,使得△PCO,△POA和△PAB中的任意两三角形都相似(全等是相似的特殊情况)?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com