
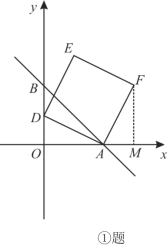
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��AB��y����x��b�ֱ���x��y�ύ��A(3��0)��B���㣮

��1����ͼ�����B�����ꣻ
��2����DΪ�߶�OB�ϵĶ��㣨��D�����O�غϣ�����ADΪ�ߣ��ڵ�һ��������������ADEF��
����ͼ�����DΪ(0��m)�����ú�m�Ĵ���ʽ��ʾ��F�����ꣻ
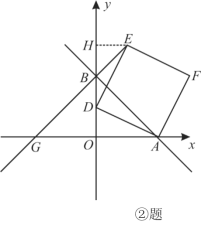
����ͼ������EB���ӳ���x���ڵ�G����D���˶�ʱ��G���λ���Ƿ����仯��������䣬�����G������ꣻ����仯����˵�����ɣ�
���𰸡���1��(0��3)����2����F(m��3��3) ���ڲ��䣬(��3��0)
��������
��1��Ҫ��B�����꣬������������ʽ��Ȼ�������ֵ���ɣ�
��2���ٸ���������ͼ���������ε�����֤������DOA�ա�AMF����m��ʾ���߳������ɱ�ʾ����F�����꣮
�ڹ�E��EH��x����H���������ε�����֤������HDE�ա�OAD������֤����BHE�ǵ���ֱ�������Σ���֤����BOGΪ����ֱ�������μ��õ������
�⣺ (1)��A(3��0)�������ֱ��AB����ʽy����x��b��
��0����3��b��
��ã�b��3��
�� ֱ��AB�Ľ���ʽΪy����x��3��
��x��0ʱ��y��3��
�� ��B�������ǣ�0��3����
(2)�ٹ�F��FM��x����M�����AMF����AOD��90����
�� �ı���ADEF�����Σ�
�� AD��AF����DAF��90����
�� ��DAO����FAM=90������AFM����FAM=90����
�� ��DAO����AFM��
�� ��DOA�ա�AMF��
�� FM��OA��3��AM��OD��m��
�� OM��m��3��
�� F(m��3��3) ��
�� G��λ�ò��䣬����Ϊ��G����3��0����
��E��EH��x����H���EHD����DOA��90����
�� �ı���ADEF�����Σ�
�� AD��DE����ADE��90����
�� ��ADO����HDE��90������ADO����DAO��90����
�� ��HDE����OAD��
�� ��HDE�ա�OAD
�� HE��OD��OA��DH��
�� OA��OB��
�� DH��OB��
�� DH��BD��BO��BD��
����BH��OD��
��HE��OD��
�� BH��HE��
�� ��BHE�ǵ���ֱ�������Σ�
�� ��HBE��45����
�� ��OBG��45����
�� ��BOGΪ����ֱ�������Σ�
�� OG��OB��3��
�� G����3��0����
��������ͬ����һ��֤��HDE�ա�OAD ��
�� HE��OD��m��OA��DH��3��
�� E(m��m��3)��
�� B(0��3)��
��ֱ��BE�Ľ���ʽΪy��kx��b
��� m��0��
��k��1��
�� ֱ��BE�Ľ���ʽΪy��x��3��
��y��0ʱ��x����3��
�� ��G��λ�ò��䣬����Ϊ����3��0����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������M��k��1��k+1������y��ĶԳƵ��ڵ��������ڣ���һ�κ���y����k��1��x+k��ͼ�����ڣ����������ޣ�
A.һB.��C.��D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Σ����ǵ��������Σ�һ����������һ�������ڶԱ��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
��1����ͼ1������ABC�У�CDΪ��ƽ���ߣ���A=40������B=60������֤��CDΪ��ABC�������ָ��ߣ�
��2������ABC�У���A=48����CD����ABC�������ָ��ߣ�����ACDΪ���������Σ����ACB�Ķ�����
��3����ͼ2����ABC�У�AC=2��BC=![]() ��CD����ABC�������ָ��ߣ�����ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
��CD����ABC�������ָ��ߣ�����ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
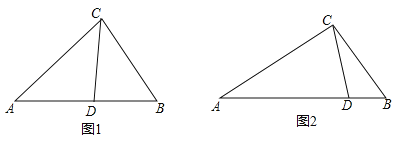
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
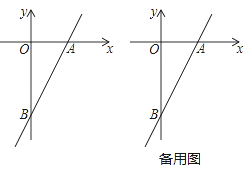
����Ŀ����֪һ�κ���y=2x��4��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B����P�ڸú���ͼ���ϣ�P��x�ᡢy��ľ���ֱ�Ϊd1��d2��
��1����PΪ�߶�AB���е�ʱ��d1+d2=_____��
��2�����P������Ϊm���ú�m�Ĵ���ʽ��ʾd1+d2������d1+d2=3ʱ��P�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����ͼ��
��1����ͼ1��ƽ���ı���ABCD����E��F�ֱ��ڱ�AD��BC�ϣ���AE��CF������EF������ֻ���̶�ֱ�����߶�EF���е�O����������ͼ�ۼ�������˵�����ɣ���
��2����ͼ2��ƽ���ı���ABCD����E�ڱ�AB�ϣ�����ֻ���̶�ֱ���ڱ�CD����һ��F��ʹ���ı���AECFΪƽ���ı��Σ���˵�����ɣ���ע�⣺�̶�ֱ��ֻ�ܹ��㻭�߶λ�ֱ�����ߣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
![]()
��1�������ϱ�ʾ![]() ��
��![]() ������֮��ľ�����__________����ʾ
������֮��ľ�����__________����ʾ![]() ��
��![]() ����֮��ľ�����__________��
����֮��ľ�����__________��
��2�����![]() ����ô
����ô![]() __________��
__________��
��3����![]() ��
��![]() ������
������![]() ��
��![]() �������ϱ�ʾ�ĵ�ֱ��ǵ�
�������ϱ�ʾ�ĵ�ֱ��ǵ�![]() ����
����![]() ����
����![]() ��
��![]() ��������������_____����������______��
��������������_____����������______��
��4�������ʽ![]() ����Сֵ����д����ʱ
����Сֵ����д����ʱ![]() ��ȡ��Щ����ֵ��
��ȡ��Щ����ֵ��
��5�������ʽ![]() ����Сֵ��
����Сֵ��
��6����![]() ��ʾһ���������������ʽ
��ʾһ���������������ʽ![]() �����ֵ�����У���������ֵ����û�У���˵�����ɣ�
�����ֵ�����У���������ֵ����û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com