
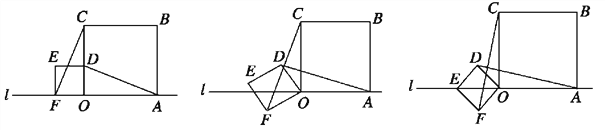
【题目】小明在数学活动课上,将边长为![]() 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
![]()
【答案】解:(1)AD=CF。理由如下:
在正方形ABCO和正方形ODEF中,∵AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF。
在△AOD和△COF中,∵AO=CO,∠AOD=∠COF,OD=OF,
∴△AOD≌△COF(SAS)。
∴AD=CF。
(2)与(1)同理求出CF=AD,
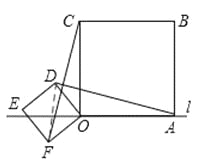
如图,连接DF交OE于G,则DF⊥OE,DG=OG=![]() OE,
OE,
∵正方形ODEF的边长为![]() ,∴OE=
,∴OE=![]() ×
×![]() =2。
=2。
∴DG=OG=![]() OE=
OE=![]() ×2=1。
×2=1。
∴AG=AO+OG=3+1=4,
在Rt△ADG中, ![]() ,
,
∴CF=AD=![]() 。
。
【解析】(1)根据正方形的性质可得AO=CO,OD=OF,∠AOC=∠DOF=90°,然后求出∠AOD=∠COF,再利用“边角边”证明△AOD和△COF全等,根据全等三角形对应边相等即可得证。
(2)与(1)同理求出CF=AD,连接DF交OE于G,根据正方形的对角线互相垂直平分可得DF⊥OE,DG=OG![]() OE,再求出AG,然后利用勾股定理列式计算即可求出AD。
OE,再求出AG,然后利用勾股定理列式计算即可求出AD。


科目:初中数学 来源: 题型:
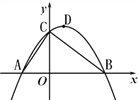
【题目】如图,已知点A的坐标为(-2,0),直线![]() 与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线
与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线![]() 过A、B、C三点.
过A、B、C三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标.
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 平行四边形的对角线相等
B. 矩形的对角线互相垂直
C. 菱形的对角线互相垂直且平分
D. 对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”期间,某公司组织员工到扬州瘦西湖旅游,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该公司有303名员工,旅行社承诺每辆车安排一名导游,导游也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助旅行社设计租车方案.
②旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游,为保证所租的每辆车均有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校七至九年级学生每天的体育锻炼时间,下列抽样调查的样本代表性较好的是
A. 选择七年级一个班进行调查
B. 选择八年级全体学生进行调查
C. 选择全校七至九年级学号是5的整数倍的学生进行调查
D. 对九年级每个班按5%的比例用抽签的方法确定调查者
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程(x﹣4)2=2x﹣3化为一般式是( )
A. x2﹣10x+13=0 B. x2﹣10x+19=0 C. x2﹣6x+13=0 D. x2﹣6x+19=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com