
【题目】小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
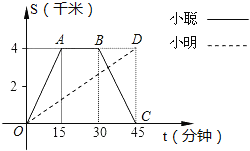
(1)小聪在天一阁查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
【答案】(1)15;![]() ;(2)s与t的函数关系式s=
;(2)s与t的函数关系式s=![]() t(0≤t≤45);(3)当小聪与小明迎面相遇时,他们离学校的路程是3千米.
t(0≤t≤45);(3)当小聪与小明迎面相遇时,他们离学校的路程是3千米.
【解析】
试题分析:(1)直接根据图象上所给的数据的实际意义可求解;
(2)由图象可知,s是t的正比例函数,设所求函数的解析式为s=kt(k≠0),把(45,4)代入解析式利用待定系数法即可求解;
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0)
把(30,4),(45,0)代入利用待定系数法先求得函数关系式,再根据求函数图象的交点方法求得交点坐标即可.
解:(1)∵30﹣15=15,4÷15=![]()
∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟,![]() 千米/分钟.
千米/分钟.
(2)由图象可知,s是t的正比例函数
设所求函数的解析式为s=kt(k≠0)
代入(45,4),得
4=45k
解得k=![]()
∴s与t的函数关系式s=![]() t(0≤t≤45).
t(0≤t≤45).
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0)
代入(30,4),(45,0),得
![]()
解得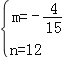
∴s=﹣![]() t+12(30≤t≤45)
t+12(30≤t≤45)
令﹣![]() t+12=
t+12=![]() t,解得t=
t,解得t=![]()
当t=![]() 时,S=
时,S=![]() ×
×![]() =3.
=3.
答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
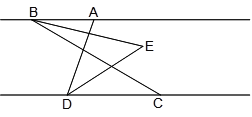
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一动点(不与A、B重合),DE⊥AC于点E,DF⊥BC于点F,点D由A向B移动时,矩形DECF的周长变化情况是( )
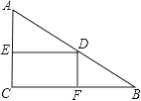
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com