
【题目】如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.
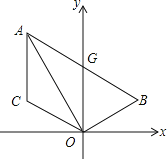
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO.
【答案】(1)等腰三角形;证明见解析;(2)证明见解析.
【解析】
(1)易证∠CAO=∠AOG和∠CAO=∠GAO,即可判定△AOG是等腰三角形;
(2)连接BC交y轴于K,过A作AN⊥y轴于N,易证△ANG≌△BKG,即可证明∠BOG=∠OBG,∠OAG=∠AOG,根据三角形内角和为180°即可解题.
解:(1)△AOG是等腰三角形;
证明:∵AC∥y轴,
∴∠CAO=∠AOG,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GAO=∠AOG,
∴AG=GO,
∴△AOG是等腰三角形;
(2)连接BC交y轴于K,过A作AN⊥y轴于N,
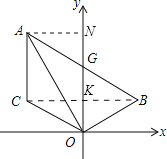
∵AC∥y轴,点B、C关于y轴对称,
∴AN=CK=BK,
在△ANG和△BKG中,
 ,
,
∴△ANG≌△BKG(AAS),
∴AG=BG,
∵AG=OG,(1)中已证,
∴AG=OG=BG,
∴∠BOG=∠OBG,∠OAG=∠AOG,
∵∠OAG+∠AOG+∠BOG+∠OBG=180°,
∴∠AOG+∠BOG=90°,
∴AO⊥BO.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
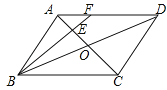
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,回答问题.
我们都知道![]() 是无理数,因为无理数是无限不循环小数,因此不可能把
是无理数,因为无理数是无限不循环小数,因此不可能把![]() 的小数部分全部写出来,于是小磊用
的小数部分全部写出来,于是小磊用![]() 表示
表示![]() 的小数部分,请你根据小磊的思路完成下列问题:
的小数部分,请你根据小磊的思路完成下列问题:
(1)![]() 的小数部分是 ;
的小数部分是 ;
(2)已知![]() 是正整数,
是正整数,![]() 是一个无理数,且
是一个无理数,且![]() 表示
表示![]() 的小数部分.
的小数部分.
①![]() 的取值范围是 ;
的取值范围是 ;
②当![]() 是5的倍数时,求
是5的倍数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
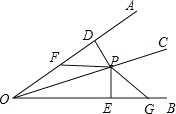
(1)求证:OC是∠AOB的平分线.
(2)若PF∥OB,且PF=4,∠AOB=30°,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
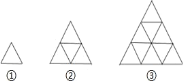
A. 63B. 60C. 56D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数![]() 的图象上.
的图象上.
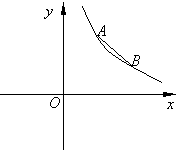
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD.有下列结论:①△AOB与△COD相似;②△ABD与△ABC相似;③S△COD∶S△AOB=DC∶AB;④S△AOD=S△BOC.其中正确的有( )
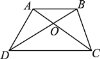
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示运算程序中,若开始输入的![]() 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
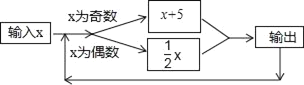
A.3B.6C.4D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com