
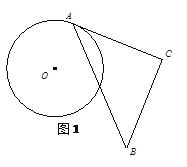
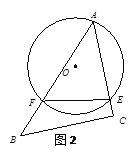
【题目】将一块含有45°的三角板ABC的顶点A放在⊙O上,且AC与⊙O相切于点A(如图1),将△ABC从点A开始,绕着点A顺时针旋转,设旋转角为α(0°<α<135°),旋转后,AC、AB分别与⊙O交于点E,F,连接EF(如图2).已知AC=8,⊙O的半径为4.
(1)在旋转过程中,有以下几个量:①弦EF的长;②![]() 的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
(2)当α=________°时,BC与⊙O相切(直接写出答案);
(3)当BC与⊙O相切时,求△AEF的面积.
【答案】(1)①②④;(2)90°;(3)16.
【解析】
试题(1)连接EO,FO,可知三角形EOF为等腰直角三角形,作OD垂直EF于D,由垂径定理,勾股定理可得出结论;(2)因为AC=8,而⊙O的半径为4.所以当BC与⊙O相切时,△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)当BC与⊙O相切时,如图:点C与点E重合,AC为⊙O直径,利用三角形AEF是等腰直角三角形得出结果.
试题解析:(1)连接EO,FO,因为∠A=45,所以∠EOF=2∠A=90,因为EO=FO,所以三角形EOF为等腰直角三角形,作OD垂直EF于D,由垂径定理得:OD垂直平分EF,三角形ODE和三角形ODF是两个全等的等腰直角三角形,所以EF=![]() OF,OD=
OF,OD=![]() OF,而半径OF是一定的,所以弦EF的长不变,点O到EF的距离即OD不变,故①④正确,又因为半径不变,圆心角∠EOF=90不变,所以
OF,而半径OF是一定的,所以弦EF的长不变,点O到EF的距离即OD不变,故①④正确,又因为半径不变,圆心角∠EOF=90不变,所以![]() 的长不变,故②正确,而∠AFE的度数等于弧AE度数的一半,A点不变,E是旋转中AC与⊙O交点,可变,故弧AE度数可变,所以∠AFE的度数可变,故③错误,所以不变的序号应是①②④;(2)因为圆的切线垂直于过切点的半径,而∠ACB=90当BC与⊙O相切时,因为AC=8,而⊙O的半径为4.所以△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)如右图,
的长不变,故②正确,而∠AFE的度数等于弧AE度数的一半,A点不变,E是旋转中AC与⊙O交点,可变,故弧AE度数可变,所以∠AFE的度数可变,故③错误,所以不变的序号应是①②④;(2)因为圆的切线垂直于过切点的半径,而∠ACB=90当BC与⊙O相切时,因为AC=8,而⊙O的半径为4.所以△ACB绕点A旋转90°后AC恰为⊙O直径,即旋转角α为90度时BC与⊙O相切;(3)如右图,
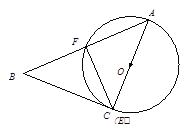
当BC与⊙O相切时,依题意可知,△ACB旋转90°后AC为⊙O直径,且点C与点E重合,∵AC为⊙O直径,∴∠AFE=90°.又∵∠BAC=45°,∴∠FCA=45°.∴∠BAC=∠FCA,∴AF=EF.∵AC=8,∴AF=EF=4![]() ,∴S△AEF=
,∴S△AEF=![]() ×(4
×(4![]() )2=16.故△AEF的面积是16..
)2=16.故△AEF的面积是16..


科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象与x轴的交点的横坐标分别为﹣1、3,则下列结论:①abc<0;②2a+b=0;③3a+2c>0;④对于任意x均有ax2﹣a+bx﹣b≥0,正确个数有( )
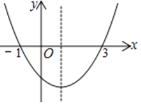
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“童舒”童装商场某种童装进价为每件60元,当售价为每件100元时,每天可卖出120件:童装的售价每上涨1元,则每天少卖2件.为了让利于顾客,商场规定销售这种重装时利润率不能超过90%,则当每件童装的售价定为多少元时,商场销售此种童装时每天可获得最大利润?每天的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b+c<0;③2a=b;④4a+2b+c>0;⑤若点(-2,y1)和(-![]() ,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
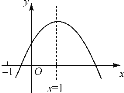
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m2-m)x2+(m-1)x+2-2m.
(1)若这个函数是二次函数,求m的取值范围.
(2)若这个函数是一次函数,求m的值.
(3)这个函数可能是正比例函数吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
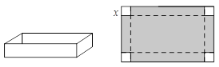
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com