
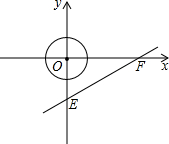
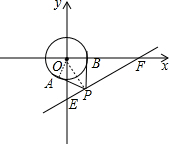
 如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2
如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| OE2+OF2 |
| 1 |
| 2 |
| 1 |
| 2 |
2×2
| ||
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
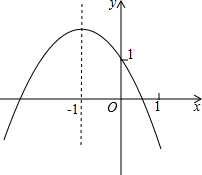 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
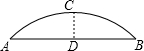 如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com