
| 1 |
| 2 |


科目:初中数学 来源: 题型:
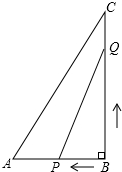 如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )
如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠BAD=∠CAD |
| C、∠B=∠C |
| D、∠ADB=∠ADC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子
将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| A、0.5 | B、1 | C、2 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )| A、30 | B、26 | C、25 | D、24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com