
 如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6.
如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6.| 1 |
| 2 |
| 1 |
| 2 |
| AG2+DG2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
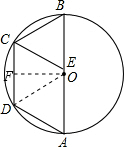 解:(1)作OF⊥DC于F,连结OC,如图,
解:(1)作OF⊥DC于F,连结OC,如图,| 1 |
| 2 |
| 1 |
| 2 |
| OD2-DF2 |
| 1 |
| 2 |
 (2)∵CD∥AB,
(2)∵CD∥AB, |
| AD |
 |
| BC |
| 1 |
| 2 |
| AG2+DG2 |
| 5 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |


科目:初中数学 来源: 题型:
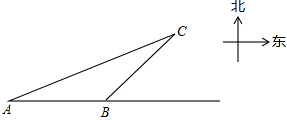 一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( )
如图,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( )| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是
a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、经过两点有且只有一条直线 |
| B、除以一个数等于乘这个数的倒数 |
| C、两个负数比较大小,绝对值大的反而小 |
| D、两点之间的所有连线中,直线最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com