练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知P（3，4）与Q（x，y）关于原点对称，则线段PQ=（　　）
    A．6B．8C．10D．7

    分析 利用关于原点对称点的性质得出Q点坐标，再利用勾股定理得出PQ的长．

    解答 解：∵P（3，4）与Q（x，y）关于原点对称，
    ∴x=-3，y=-4，
    ∴Q（-3，-4），
    则线段PQ=$\sqrt{{6}^{2}+{8}^{2}}$=10．
    故选：C．

    点评 此题主要考查了关于原点对称点的性质，熟练应用勾股定理是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

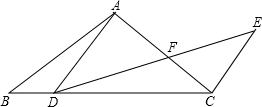    7．如图，在△ABC中，AB=AC=10，cosB=$\frac{4}{5}$，点D、F为边BC、AC上一点，∠ADF=∠B，BD=4．
    （1）求FC的长；
    （2）若AD∥CE，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某农场第一车间有x人，第二车间比第一车间人数的$\frac{4}{5}$少30人，那么：
    （1）两个车间共有$\frac{9}{5}$x-30人？
    （2）如果从第二车间调出10人到第一车间，调动后，第一车间的人数为x+10人，第二车间的人数为$\frac{4}{5}$x-40人．
    （3）求调动后，第一车间的人数比第二车间的人数多几人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．定义：如果一元二次方程ax2+bx+c=0（a≠0）满足a+b+c=0，那么我们称这个方程为“凤凰”方程．已知x2+mx+n=0是“凤凰”方程，且有两个相等的实数根，求m2+n2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．方程（x+1）（x-2）=0的两根分别为（　　）
    A．x1=1，x2=2B．x1=-1，x2=-2C．x1=1，x2=-2D．x1=-1，x2=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．我市某风景区今年9月份上缴税收100万元，10月份上缴的已增加，11月份准备上缴税收121万元，若从9月份至11月份的2个月中，每月上缴的平均增长率一样，求月平均增长率．（用一元二次方程求解）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

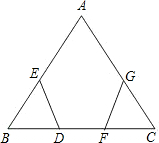    9．如图，一个特大型设备人字梁，工人师傅要检查人字梁的AB和AC是否相等，但是他直接测量不方便，身边只有一个刻度尺（长度远远不够）．它是这样操作的：①分别在BA和CA上取BE=CG；②在BC上取BD=CF；③量出DE的长a米，FG的长b米，如果a=b，则说明AB和AC是相等的，他的这种做法合理吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．要做一个容积是1500cm3，高是10cm，底面的长比宽多5cm的长方体匣子，求底面的长和宽．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．钟表问题：
    （1）3点时，时针与分针的夹角为90°；
    （2）3点半时，时针与分针的夹角为75°；
    （3）2点40分时，时针与分针的夹角为160°；
    （4）8点35分时，时针与分针的夹角为164.5°．

    查看答案和解析>>

    同步练习册答案