
 如图,将矩形ABCD纸片对折,设折痕为MN,再通过折叠使B点落在折线段MN上的B',设两条线段的交点为F,连接BF、EB'、FB'、AB'.
如图,将矩形ABCD纸片对折,设折痕为MN,再通过折叠使B点落在折线段MN上的B',设两条线段的交点为F,连接BF、EB'、FB'、AB'.分析 (1)根据直角三角形的性质得到∠AB′M=30°,根据翻转变换的性质得到AB=AB′,得到△ABB'是等边三角形,得到答案;
(2)根据余弦的定义出去AE,根据四边形的面积公式计算即可.
解答 解:(1)由折叠的性质可知,AB=AB′,AM=$\frac{1}{2}$AB,
∴AM=$\frac{1}{2}$AB′,又∠AMB′=90°,
∴∠AB′M=30°,
∴∠B′AB=60°,
∴△ABB'是等边三角形,
∴∠ABB'=60°;
(2)∵∠BAE=30°,AB=4,
∴AE=$\frac{AB}{cos∠BAE}$=$\frac{8\sqrt{3}}{3}$,
∴EF=$\frac{4\sqrt{3}}{3}$,
∴四边形BFB'E的面积=$\frac{1}{2}$×BB′×EF=$\frac{8\sqrt{3}}{3}$.
点评 本题考查的是翻转变换的性质、等边三角形的判定,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是用棋子摆成的“H”字,摆成第一个“H”字需要7枚棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为( )
如图是用棋子摆成的“H”字,摆成第一个“H”字需要7枚棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为( )| A. | 5x | B. | 5x-1 | C. | 5x+2 | D. | 5x+5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
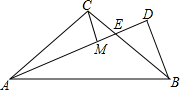 如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.
如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
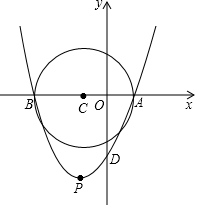 如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.
如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com