
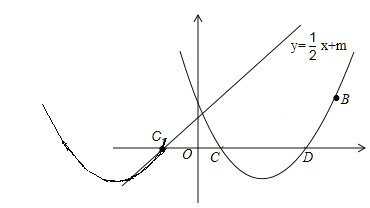
【题目】在平面直角坐标系xOy中,抛物线![]() ,与x轴交于点C,
,与x轴交于点C,![]() 点C在点D的左侧
点C在点D的左侧![]() ,与y轴交于点A.
,与y轴交于点A.
![]() 求抛物线顶点M的坐标;
求抛物线顶点M的坐标;
![]() 若点A的坐标为
若点A的坐标为![]() ,
,![]() 轴,交抛物线于点B,求点B的坐标;
轴,交抛物线于点B,求点B的坐标;
![]() 在
在![]() 的条件下,将抛物线在B,C两点之间的部分沿y轴翻折,翻折后的图象记为G,若直线
的条件下,将抛物线在B,C两点之间的部分沿y轴翻折,翻折后的图象记为G,若直线![]() 与图象G有一个交点,结合函数的图象,求m的取值范围.
与图象G有一个交点,结合函数的图象,求m的取值范围.
【答案】(1)M的坐标为![]() ;(2)B(4,3);(3)
;(2)B(4,3);(3)![]() 或
或![]() .
.
【解析】
![]() 利用配方法将已知函数解析式转化为顶点式方程,可以直接得到答案
利用配方法将已知函数解析式转化为顶点式方程,可以直接得到答案![]()
![]() 根据抛物线的对称性质解答;
根据抛物线的对称性质解答;
![]() 利用待定系数法求得抛物线的表达式为
利用待定系数法求得抛物线的表达式为![]() 根据题意作出图象G,结合图象求得m的取值范围.
根据题意作出图象G,结合图象求得m的取值范围.
解:(1)![]() ,
,
![]() 该抛物线的顶点M的坐标为
该抛物线的顶点M的坐标为![]() ;
;
![]() 由
由![]() 知,该抛物线的顶点M的坐标为
知,该抛物线的顶点M的坐标为![]() ;
;
![]() 该抛物线的对称轴直线是
该抛物线的对称轴直线是![]() ,
,
![]() 点A的坐标为
点A的坐标为![]() ,
,![]() 轴,交抛物线于点B,
轴,交抛物线于点B,
![]() 点A与点B关于直线
点A与点B关于直线![]() 对称,
对称,
![]() ;
;
![]() 抛物线
抛物线![]() 与y轴交于点
与y轴交于点![]() ,
,
![]() .
.
![]() .
.
![]() 抛物线的表达式为
抛物线的表达式为![]() .
.
![]() 抛物线G的解析式为:
抛物线G的解析式为:![]()
由![]() .
.
由![]() ,得:
,得:![]()
![]() 抛物线
抛物线![]() 与x轴的交点C的坐标为
与x轴的交点C的坐标为![]() ,
,
![]() 点C关于y轴的对称点
点C关于y轴的对称点![]() 的坐标为
的坐标为![]() .
.
把![]() 代入
代入![]() ,得:
,得:![]() .
.
把![]() 代入
代入![]() ,得:
,得:![]() .
.
![]() 所求m的取值范围是
所求m的取值范围是![]() 或
或![]() .
.
故答案为:(1)M的坐标为![]() ;(2)B(4,3);(3)
;(2)B(4,3);(3)![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
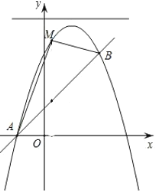
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CEAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
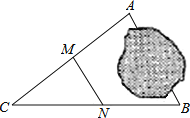
A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(请将下面2小题的结果都精确到0.1米,参考数据![]() ).
).
【1】若修建的斜坡BE的坡角(即∠BAC)不大于45°,则平台DE的长最多为 ▲ 米;
【2】一座建筑物GH距离坡脚A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面上,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
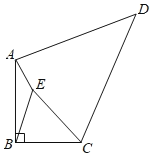
【题目】如图,在四边形ABCD中,∠B=90°,∠D=45°,AB=BC=2,点E为四边形ABCD内部一点,且满足CE2﹣AE2=2BE2,则点E在运动过程中所形成的图形的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活,为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:


(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
(5)学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组,求出恰好选中是体育和科普两类的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
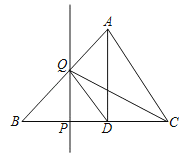
【题目】如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA﹣AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com