
分析 此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长.
解答 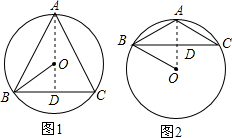 解:如图1,当△ABC是锐角三角形时,连接AO并延长到BC于点D,
解:如图1,当△ABC是锐角三角形时,连接AO并延长到BC于点D,
∵AB=AC,O为外心,
∴AD⊥BC,
在Rt△BOD中,
∵OB=10,OD=6,
∴BD=$\sqrt{{OB}^{2}-{OD}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8.
在Rt△ABD中,根据勾股定理,得AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=$\sqrt{{16}^{2}+{8}^{2}}$=8$\sqrt{5}$(cm);
如图2,当△ABC是钝角或直角三角形时,连接AO交BC于点D,
在Rt△BOD中,
∵OB=10,OD=6,
∴BD=$\sqrt{{OB}^{2}-{OD}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8,
∴AD=10-6=4,
在Rt△ABD中,根据勾股定理,得AB=$\sqrt{{BD}^{2}+{AD}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$(cm).
故答案为:8$\sqrt{5}$或4$\sqrt{5}$.
点评 本题考查的是垂径定理,在解答此题时要注意进行分类讨论,不要漏解.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
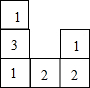 右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的主视图是( )
右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的主视图是( )| A. | 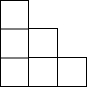 | B. | 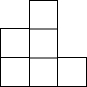 | C. | 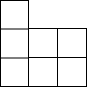 | D. | 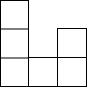 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k>-1且k≠0 | C. | k>1且k≠2 | D. | k<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
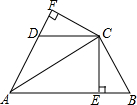 已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
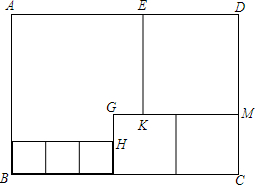 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm.
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com