
【题目】如图,直线![]() ,点
,点![]() 在直线
在直线![]() 与
与![]() 之间,点
之间,点![]() 在直线
在直线![]() 上,连结
上,连结![]() .
.![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的度数是__________.
的度数是__________.

【答案】27°.
【解析】
设∠DAE=α,则∠EAF=α,∠ACB=![]() α,先求得∠BCE+∠CEA=180°,即可得到AE//BC,进而得出∠ACB=∠CAE,即可得到∠DAE=18°,再依据Rt△ACD内角和即可得到∠ACD的度数.
α,先求得∠BCE+∠CEA=180°,即可得到AE//BC,进而得出∠ACB=∠CAE,即可得到∠DAE=18°,再依据Rt△ACD内角和即可得到∠ACD的度数.
设∠DAE=α,则∠EAF=α,∠ACB=![]() α,
α,
∵AD⊥PQ,AF⊥AB,
∴∠BAF=∠ADE=90°,
∴∠BAE=∠BAF+∠EAF=90°+α,∠CEA=∠ADE+∠DAE=90°+α,
∴∠BAE=∠CAE,
∵MN//PQ,BC平分∠ABM,
∴∠BCE=∠CBM=∠CBA,
又∵∠ABC+∠BCE+∠CEA+∠BAE=360°,
∴∠BCE+∠CEA=180°,
∴AE//BC,
∴∠ACB=∠CAE,即![]() α=45°,
α=45°,
∴α=18°,
∴∠DAE=18°,
∴Rt△ACD中,∠ACD=90°∠CAD=90°(45°+18°)=27°,
故答案为:27°.


科目:初中数学 来源: 题型:
【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图的统计图(图中信息不完整).已知A,B两组捐款人数的比为1∶5.
捐款人数分组统计表
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
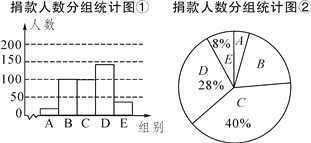
请结合以上信息解答下列问题:
(1)a=____,本次调查的样本容量是______;
(2)先求出C组的人数,再补全“捐款人数分组统计图①;
(3)若该学校自愿捐款的学生有1500人,请估计捐款不少于30元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;
方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%
(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?
(注:投资收益率=![]() ×100%)
×100%)
(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元.问甲乙两人各投资了多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,![]() 表示行驶里程,
表示行驶里程,![]() (元)表示车费,请根据图象回答下列问题:
(元)表示车费,请根据图象回答下列问题:
(1)出租车的起步价是多少元;
(2)当 ![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各位数的和是7,![]() 再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.
(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
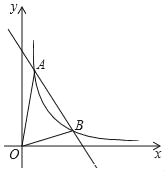
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com