
【题目】如图,直线![]() ,连接
,连接![]() ,
,![]() 为一动点.
为一动点.
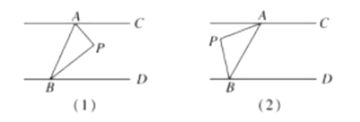
(1)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,求证:
,求证:![]() ;
;
(2)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,则
,则![]() 之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
【答案】(1)见解析(2)∠APB+∠PAC+∠PBD=360![]()
【解析】
(1)延长AP交BD于M,根据三角形外角性质和平行线性质得出∠APB=∠AMB+∠PBD,∠PAC=∠AMB,代入求出即可;
(2)过P作EF∥AC,根据平行线性质得出∠PAC+∠APF=180![]() ,∠PBD+∠BPF=180
,∠PBD+∠BPF=180![]() ,即可得出答案.
,即可得出答案.
(1)延长AP交BD于M,如图1,

∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)∠APB+∠PAC+∠PBD=360![]() ,
,
如图2,过P作EF∥AC,
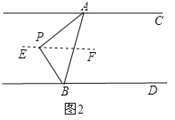
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180![]() ,∠PBD+∠BPF=180
,∠PBD+∠BPF=180![]() ,
,
∴∠PAC+∠APF+∠PBD+∠BPF=360![]() ,
,
∴∠APB+∠PAC+∠PBD=360![]() ,
,
∴∠APB+∠PAC+∠PBD=360![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
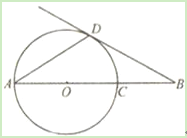
【题目】如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.
(1)直线BD是否与⊙O相切?为什么?
(2)连接CD,若CD=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.则∠D的度数为( )

A.15°B.17.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
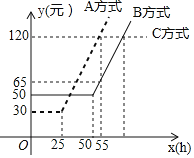
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
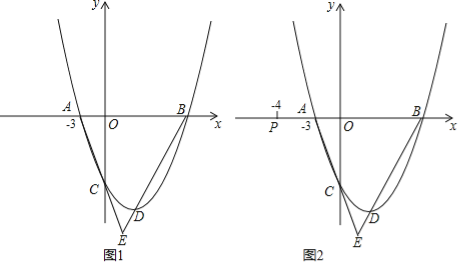
(1)求D点的坐标;
(2)如图1,连接AC,BD并延长交于点E,求∠E的度数;
(3)如图2,已知点P(﹣4,0),点Q在x轴下方的抛物线上,直线PQ交线段AC于点M,当∠PMA=∠E时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= ![]() .
.
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=![]() =
=![]() .
.
特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
(2)已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,
试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com